Segmentace MRI mozku - U-Net model
V předchozích několika článcích jsem se zabýval problémem klasifikace RTG snímků. Ve své podstatě jsem hledal odpověď na otázku, zda je na konkrétním RTG snímku možné rozpoznat zápal plic pacienta nebo nikoliv (jednalo se tedy o binární klasifikaci s odpovědí ano/ne).
Co kdyby mne zajímala odpověď na otázku, ve kterém konkrétním místě ten problém je. Chtěl bych vidět místo na obrázku, které vede k závěru, že pacient danou nemoc má. Takovýto problém se označuje jako segmentace, a v tomto případě se jedná o tzv. sémantickou segmentaci (hledám oblasti na obrázku, které spadají do jedné společné třídy).
Pro své experimentování s modely jsem si vybral opět jednu z velice oblíbených datových sad pro tento účel. Jedná se o datovou sadu Brain MRI segmentation, která obsahuje snímky magnetické rezonance mozku (MRI). Datová sada obsahuje jednotlivé řezy MRI a k nim přiřazené binární masky vyznačující oblast s nádorem.
Chtěl bych vytvořit model, který by mně zkusil na neznámém snímku vyznačit co nejpřesněji oblast s předpokládaným nádorem, pokud tam tedy skutečně je. Při detailnějším pohledu na obsah datové sady bude asi zřejmější, před čím konkrétně stojíme (viz. následující kapitola).
Dnes bych se chtěl zaměřit na jeden z nejčastěji citovaných modelů pro tento účel, a sice tzv. U-Net. Jedná se o model postavený plně na konvolučních vrstvách, vycházející z archetypu encoder-decoder. O tom bych chtěl povídat více až při implementaci samotného modelu.
In [1]:
import sys import os import shutil import warnings import glob import pathlib import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.model_selection import train_test_split import tensorflow as tf import tensorflow.keras as keras from keras.models import Sequential from keras import Input, Model from keras import layers import cv2 sns.set_style('darkgrid') warnings.simplefilter(action='ignore', category=FutureWarning)
In [2]:
def seed_all():
import random
random.seed(42)
np.random.seed(42)
tf.random.set_seed(42)
os.environ['PYTHONHASHSEED'] = str(42)
os.environ['TF_DETERMINISTIC_OPS'] = '1'
seed_all()
V prvém kroku nezbytné konstanty. Cesta ke kořenu datové sady je zřejmá. Nicméně již dopředu musím uvést, že obrázky budu z datové sady načítat ve zmenšené velikosti 128×128 pixelů (originální rozlišení je 256×256). Důvodem je opět potřeba eliminovat požadavky na velikost paměti při trénování modelu. Ze stejného důvodu jsem musel i omezovat hloubku konvolučních vrstev. Jinak řečeno, výsledky segmentace by mohly být v cílovém stavu asi lepší, ale o to mně až tak v tomto článku nejde.
In [3]:
DATA_ROOT = "/kaggle/input/lgg-mri-segmentation/kaggle_3m/"
IMAGE_SIZE = (128, 128)
Datová sada Brain MRI segmentation
V prvém kroku si potřebuji „spárovat“ každý MRI řez s jemu odpovídající segmentační maskou. V případě této datové sady je to uděláno jednoduše na základě názvu souboru:
In [4]:
image_paths = [] for path in glob.glob(DATA_ROOT + "**/*_mask.tif"): def strip_base(p): parts = pathlib.Path(p).parts return os.path.join(*parts[-2:]) image = path.replace("_mask", "") if os.path.isfile(image): image_paths.append((strip_base(image), strip_base(path))) else: print("MISSING: ", image, "==>", path)
Vždy je dobré se podívat na nějaké vybrané vzorky. Zde jsou některé z nich s promítnutou odpovídající maskou nádoru:
In [5]:
rows, cols = 3, 3 fig=plt.figure(figsize=(12, 12)) for i in range(1, rows*cols+1): fig.add_subplot(rows, cols, i) img_path, mask_path = image_paths[i] img = cv2.imread(DATA_ROOT + img_path, flags=cv2.IMREAD_COLOR) img = cv2.resize(img, IMAGE_SIZE) # img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) msk = cv2.imread(DATA_ROOT + mask_path, flags=cv2.IMREAD_GRAYSCALE) msk = cv2.resize(msk, IMAGE_SIZE) plt.imshow(img) plt.imshow(msk, alpha=0.4) plt.show()
A nyní si již můžu vše načíst do paměti jako numpy pole. V proměnné X budu mít pole s jednotlivými MRI skeny, v poli Y pak jim odpovídající binární masky:
In [6]:
def get_image_data(image_paths):
x, y = list(), list()
for image_path, mask_path in image_paths:
image = cv2.imread(os.path.join(DATA_ROOT, image_path), flags=cv2.IMREAD_COLOR)
image = cv2.resize(image, IMAGE_SIZE)
mask = cv2.imread(os.path.join(DATA_ROOT, mask_path), flags=cv2.IMREAD_GRAYSCALE)
mask = cv2.resize(mask, IMAGE_SIZE)
x.append(image)
y.append(mask)
return np.array(x) / 255, np.expand_dims(np.array(y) / 255, -1)
X, Y = get_image_data(image_paths)
print("X: ", X.shape)
print("Y: ", Y.shape)
X: (3929, 128, 128, 3)
Y: (3929, 128, 128, 1)
Z rozměrů polí vyplývá, že jsem načetl celkem 3929 vzorků s rozměrem 128×128 bodů. V případě MRI skenů jsem je načetl jako RGB snímky se třemi kanály. V případě masek se jedná o snímky s jedním kanálem pro rozlišení šedi. Navíc jsou všechny hodnoty v polích standardizovány do rozsahu <0, 1>.
U-Net Model
Dostávám se k samotnému modelu. Nejdříve asi ukážu základní schéma, jak se model zobrazuje:
Model vychází ze základní architektury Encoder-Decoder.
Na levé straně schématu vidíte část Encoder, tady se tomu také říká kontrakční fáze. Ta by vám měla být dost povědomá. Je založena na klasifikačních modelech, kterými jsem se již v několika předchozích článcích zabýval. V tomto případě se vychází z klasifikačního modelu VGG, ale pochopitelně jde použít i jiné podobné modely. V podstatě jde o to, že v jednotlivých konvolučních blocích postupně redukuji rozměry obrázků, a současně zvětšuji počet extrahovaných vlastností.
Celé to probíhá až do tzv. úzkého místa, kde jsou prostorové rozměry nejmenší (ne však nulové) a počty vlastností největší.
A zde se přehoupnu do pravé strany schématu, tedy na část Decoder nebo také expanzní fázi. Proces zrcadlově kopíruje levou stranu, takže postupně zvětšuji rozměry obrázků a omezuji počty vlastní. A to vše tak dlouho, dokud ne nedostanu na původní rozměry obrázků. Jak ale probíhá rozšíření prostorových rozměrů? Za tímto účelem se v tomto případě používá tzv. transpose convolution, která promítá jeden bod do obdélníku přes filtry. Aby se dosáhlo zdvojnásobení rozměrů, používá se krok konvoluce 2.
Takto postavený model by mně ale moc nefungoval. Při kontrakční fázi jsem postupně ztrácel informaci o prostorovém uspořádání vlastností. Musím tuto informaci nějak dostat zpět do expanzní fáze. Pro vyřešení tohoto problému jsou ve schématu ještě tzv. skip connection. Ty by vám mohly být povědomé z modelu ResNet. Po každém rozšíření plošných rozměrů pomocí transpose convolution se její výstup spojí s výstupem z odpovídající vrstvy kontrakční fáze (prostě se ty tensory slepí k sobě). Vznikne tensor s dvojnásobným počtem vlastností, které se ale následnou konvolucí opět srazí dolů.
K popisu mně chybí ještě výstupní vrstva. V průběhu expanze jsem se dostal až na rozměry původního obrázku. Co ale bude hodnotou jednoho bodu? V mém případě hledám pro každý bod obrázku pravděpodobnost, že bod reprezentuje nádor nebo nikoliv. Takže mou poslední vrstvou bude konvoluce se jediným filtrem a aktivační funkcí sigmoid.
A to je celé. Pro zájemce připojuji ještě několik odkazů na články a zdroje, které by vám mohly pomoci při detailnějším bádání:
-
https://www.analyticsvidhya.com/blog/2023/08/unet-architecture-mastering-image-segmentation/
-
https://towardsdatascience.com/types-of-convolutions-in-deep-learning-717013397f4d
Všechna data, která mám k dispozici, si rozdělím na sady pro trénování a testování:
In [7]:
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)
Touto funkcí si vytvořím samotný U-Net model. Nejdříve opět výpis a následně pak několik poznámek k implementaci:
In [8]:
def create_model_UNet(X_shape, classes=1, name="UNet"):
def conv_block(x, *, filters, kernel_size=(3, 3), strides=(1, 1), padding='same', activation='relu', name=""):
x = layers.Conv2D(filters=filters, kernel_size=kernel_size, strides=strides, padding=padding, kernel_initializer="he_normal", name=f"{name}_conv")(x)
x = layers.BatchNormalization(name=f"{name}_norm")(x)
if activation:
x = layers.Activation(activation, name=f"{name}_acti")(x)
return x
def encoder_block(x, *, filters, name=""):
x = conv_block(x, filters=filters, name=f"{name}_conv1")
x = conv_block(x, filters=filters, name=f"{name}_conv2")
return layers.MaxPooling2D((2, 2), strides=2, name=f'{name}_maxpool')(x), x
def decoder_block(x, s, *, filters, name=""):
x = layers.Conv2DTranspose(filters, (2, 2), strides=2, padding='same', kernel_initializer="he_normal", name=f"{name}_trans")(x)
x = layers.Concatenate(name=f"{name}_concat")([x, s])
x = conv_block(x, filters=filters, name=f"{name}_conv1")
x = conv_block(x, filters=filters, name=f"{name}_conv2")
return x
# Input
inputs = Input(X_shape[-3:], name='inputs')
# Contracting Path
e1, s1 = encoder_block(inputs, filters=64, name="enc1")
e2, s2 = encoder_block(e1, filters=128, name="enc2")
e3, s3 = encoder_block(e2, filters=256, name="enc3")
e4, s4 = encoder_block(e3, filters=512, name="enc4")
# Bottleneck
b1 = conv_block(e4, filters=1024, name="bot1")
b2 = conv_block(b1, filters=1024, name="bot2")
# Expansive Path
d4 = decoder_block(b2, s4, filters=512, name="dec1")
d3 = decoder_block(d4, s3, filters=256, name="dec2")
d2 = decoder_block(d3, s2, filters=128, name="dec3")
d1 = decoder_block(d2, s1, filters=64, name="dec4")
# Output
outputs = conv_block(d1, filters=classes, kernel_size=(1, 1), activation='sigmoid', name="outputs")
return Model(inputs=inputs, outputs=outputs, name=name)
Model budu postupně skládat se dvou typů bloků.
Pro kontrakční fázi je připraven encoder_block, který obsahuje dva identické konvoluční bloky zakončené jednou vrstvou MaxPooling2D. Ta zajišťuje redukci prostorových dimenzí na polovinu. Výsledek bloku je dvojice tenzorů, kdy prvním je po redukci prostorových dimenzí, a ten druhý je před redukcí. Druhý se použije jako „skip connection“ do expanzní fáze. Celá kontrakční fáze v mém případě obsahuje čtyři bloky, což mně zajistí redukci obrázku do dimenze 8×8×512.
Následuje úzké hrdlo tvořené dvěma konvolučními bloky, které udržují rozměry obrázku, ale ještě mně rozšířily počty vlastností, takže výsledný rozměr je 8×8×1024.
Na hrdlo navazuje expanzní fáze, která je tvořena čtyřmi decoder_block. Vstupem do dekoder_block je nejen výstup předchozího bloku, ale také uschovaná „skip connection“ z kontrakční fáze. V bloku nejdříve provedu rozšíření prostorových dimenzí pomocí Con2DTranspose vrstvy. Výsledek pak spojím s tenzorem ze skip connection, a následně ještě pošlu do dvou identických konvolučních bloků.
Celý model je zakončen posledním konvolučním blokem s počtem filtrů odpovídajícím třídám, v mém případě to je 1, a aktivační funkcí sigmoid.
A to je celý model.
Vyhodnocení modelu
Specifické ztrátové funkce a metriky
Pro trénování modelu potřebuji definovat ztrátovou funkci, která se bude při trénování optimalizovat. Pro tento účel je možné použít CrossEntropy ( v tomto konkrétním případě by to byla Binary CrossEntropy). Nicméně pro segmentaci se používají i jiné ztrátové funkce založené na metrikách Dice Coefficient nebo Jaccard Index. Pokud by vás zajímalo více informací, jak jsou tyto metriky definované, pak jeden ze zdrojů informací by mohl být Understanding Evaluation Metrics in Medical Image Segmentation.
Dále je uvedena implementace pro Dice Coefficient i Jaccard Index, a to pro použití jako ztrátová funkce nebo jako metrika. Já jsem dále pro své experimenty použil kombinaci Binary-CrossEntropy a Dice Coefficient (funkce bce_dice_loss).
Implementace jsem si vypůjčil a částečně modifikoval z: https://github.com/shruti-jadon/Semantic-Segmentation-Loss-Functions/tree/master
In [9]:
import keras.backend as K from keras.losses import binary_crossentropy def dsc(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = K.sum(y_true_f * y_pred_f) score = (2. * intersection + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return score def dice_loss(y_true, y_pred): loss = 1 - dsc(y_true, y_pred) return loss def bce_dice_loss(y_true, y_pred): loss = binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) return loss def jaccard_similarity(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = K.sum(y_true_f * y_pred_f) + smooth union = K.sum((y_true_f + y_pred_f) - (y_true_f * y_pred_f)) + smooth return intersection / union def jaccard_loss(y_true, y_pred): return 1 - jaccard_similarity(y_true, y_pred)
Překlad modelu
V následujícím kroku si již model můžu vytvořit a přeložit.
Jak jsem uvedl dříve, jako ztrátovou funkci jsem použil bce_dice_loss. Metriky pro vyhodnocení jsem použil dvě, Accuracy a Dice Coefficient.
Tu metriku Accuracy jsem tam nechal schválně. Jak uvidíte z výsledků trénování, je úplně nanic. Je to pěkný příklad toho, jak si dát pozor na výběr metrik vhodných pro konkrétní účel a konkrétní data.
In [10]:
model = create_model_UNet(x_test.shape, 1) model.compile(optimizer="adam", loss=bce_dice_loss, metrics=['accuracy', dsc]) model.summary() Model: "UNet" __________________________________________________________________________________________________ Layer (type) Output Shape Param # Connected to ================================================================================================== inputs (InputLayer) [(None, 128, 128, 3)] 0 [] enc1_conv1_conv (Conv2D) (None, 128, 128, 64) 1792 ['inputs[0][0]'] enc1_conv1_norm (BatchNorm (None, 128, 128, 64) 256 ['enc1_conv1_conv[0][0]'] alization) enc1_conv1_acti (Activatio (None, 128, 128, 64) 0 ['enc1_conv1_norm[0][0]'] n) enc1_conv2_conv (Conv2D) (None, 128, 128, 64) 36928 ['enc1_conv1_acti[0][0]'] enc1_conv2_norm (BatchNorm (None, 128, 128, 64) 256 ['enc1_conv2_conv[0][0]'] alization) enc1_conv2_acti (Activatio (None, 128, 128, 64) 0 ['enc1_conv2_norm[0][0]'] n) enc1_maxpool (MaxPooling2D (None, 64, 64, 64) 0 ['enc1_conv2_acti[0][0]'] ) enc2_conv1_conv (Conv2D) (None, 64, 64, 128) 73856 ['enc1_maxpool[0][0]'] enc2_conv1_norm (BatchNorm (None, 64, 64, 128) 512 ['enc2_conv1_conv[0][0]'] alization) enc2_conv1_acti (Activatio (None, 64, 64, 128) 0 ['enc2_conv1_norm[0][0]'] n) enc2_conv2_conv (Conv2D) (None, 64, 64, 128) 147584 ['enc2_conv1_acti[0][0]'] enc2_conv2_norm (BatchNorm (None, 64, 64, 128) 512 ['enc2_conv2_conv[0][0]'] alization) enc2_conv2_acti (Activatio (None, 64, 64, 128) 0 ['enc2_conv2_norm[0][0]'] n) enc2_maxpool (MaxPooling2D (None, 32, 32, 128) 0 ['enc2_conv2_acti[0][0]'] ) enc3_conv1_conv (Conv2D) (None, 32, 32, 256) 295168 ['enc2_maxpool[0][0]'] enc3_conv1_norm (BatchNorm (None, 32, 32, 256) 1024 ['enc3_conv1_conv[0][0]'] alization) enc3_conv1_acti (Activatio (None, 32, 32, 256) 0 ['enc3_conv1_norm[0][0]'] n) enc3_conv2_conv (Conv2D) (None, 32, 32, 256) 590080 ['enc3_conv1_acti[0][0]'] enc3_conv2_norm (BatchNorm (None, 32, 32, 256) 1024 ['enc3_conv2_conv[0][0]'] alization) enc3_conv2_acti (Activatio (None, 32, 32, 256) 0 ['enc3_conv2_norm[0][0]'] n) enc3_maxpool (MaxPooling2D (None, 16, 16, 256) 0 ['enc3_conv2_acti[0][0]'] ) enc4_conv1_conv (Conv2D) (None, 16, 16, 512) 1180160 ['enc3_maxpool[0][0]'] enc4_conv1_norm (BatchNorm (None, 16, 16, 512) 2048 ['enc4_conv1_conv[0][0]'] alization) enc4_conv1_acti (Activatio (None, 16, 16, 512) 0 ['enc4_conv1_norm[0][0]'] n) enc4_conv2_conv (Conv2D) (None, 16, 16, 512) 2359808 ['enc4_conv1_acti[0][0]'] enc4_conv2_norm (BatchNorm (None, 16, 16, 512) 2048 ['enc4_conv2_conv[0][0]'] alization) enc4_conv2_acti (Activatio (None, 16, 16, 512) 0 ['enc4_conv2_norm[0][0]'] n) enc4_maxpool (MaxPooling2D (None, 8, 8, 512) 0 ['enc4_conv2_acti[0][0]'] ) bot1_conv (Conv2D) (None, 8, 8, 1024) 4719616 ['enc4_maxpool[0][0]'] bot1_norm (BatchNormalizat (None, 8, 8, 1024) 4096 ['bot1_conv[0][0]'] ion) bot1_acti (Activation) (None, 8, 8, 1024) 0 ['bot1_norm[0][0]'] bot2_conv (Conv2D) (None, 8, 8, 1024) 9438208 ['bot1_acti[0][0]'] bot2_norm (BatchNormalizat (None, 8, 8, 1024) 4096 ['bot2_conv[0][0]'] ion) bot2_acti (Activation) (None, 8, 8, 1024) 0 ['bot2_norm[0][0]'] dec1_trans (Conv2DTranspos (None, 16, 16, 512) 2097664 ['bot2_acti[0][0]'] e) dec1_concat (Concatenate) (None, 16, 16, 1024) 0 ['dec1_trans[0][0]', 'enc4_conv2_acti[0][0]'] dec1_conv1_conv (Conv2D) (None, 16, 16, 512) 4719104 ['dec1_concat[0][0]'] dec1_conv1_norm (BatchNorm (None, 16, 16, 512) 2048 ['dec1_conv1_conv[0][0]'] alization) dec1_conv1_acti (Activatio (None, 16, 16, 512) 0 ['dec1_conv1_norm[0][0]'] n) dec1_conv2_conv (Conv2D) (None, 16, 16, 512) 2359808 ['dec1_conv1_acti[0][0]'] dec1_conv2_norm (BatchNorm (None, 16, 16, 512) 2048 ['dec1_conv2_conv[0][0]'] alization) dec1_conv2_acti (Activatio (None, 16, 16, 512) 0 ['dec1_conv2_norm[0][0]'] n) dec2_trans (Conv2DTranspos (None, 32, 32, 256) 524544 ['dec1_conv2_acti[0][0]'] e) dec2_concat (Concatenate) (None, 32, 32, 512) 0 ['dec2_trans[0][0]', 'enc3_conv2_acti[0][0]'] dec2_conv1_conv (Conv2D) (None, 32, 32, 256) 1179904 ['dec2_concat[0][0]'] dec2_conv1_norm (BatchNorm (None, 32, 32, 256) 1024 ['dec2_conv1_conv[0][0]'] alization) dec2_conv1_acti (Activatio (None, 32, 32, 256) 0 ['dec2_conv1_norm[0][0]'] n) dec2_conv2_conv (Conv2D) (None, 32, 32, 256) 590080 ['dec2_conv1_acti[0][0]'] dec2_conv2_norm (BatchNorm (None, 32, 32, 256) 1024 ['dec2_conv2_conv[0][0]'] alization) dec2_conv2_acti (Activatio (None, 32, 32, 256) 0 ['dec2_conv2_norm[0][0]'] n) dec3_trans (Conv2DTranspos (None, 64, 64, 128) 131200 ['dec2_conv2_acti[0][0]'] e) dec3_concat (Concatenate) (None, 64, 64, 256) 0 ['dec3_trans[0][0]', 'enc2_conv2_acti[0][0]'] dec3_conv1_conv (Conv2D) (None, 64, 64, 128) 295040 ['dec3_concat[0][0]'] dec3_conv1_norm (BatchNorm (None, 64, 64, 128) 512 ['dec3_conv1_conv[0][0]'] alization) dec3_conv1_acti (Activatio (None, 64, 64, 128) 0 ['dec3_conv1_norm[0][0]'] n) dec3_conv2_conv (Conv2D) (None, 64, 64, 128) 147584 ['dec3_conv1_acti[0][0]'] dec3_conv2_norm (BatchNorm (None, 64, 64, 128) 512 ['dec3_conv2_conv[0][0]'] alization) dec3_conv2_acti (Activatio (None, 64, 64, 128) 0 ['dec3_conv2_norm[0][0]'] n) dec4_trans (Conv2DTranspos (None, 128, 128, 64) 32832 ['dec3_conv2_acti[0][0]'] e) dec4_concat (Concatenate) (None, 128, 128, 128) 0 ['dec4_trans[0][0]', 'enc1_conv2_acti[0][0]'] dec4_conv1_conv (Conv2D) (None, 128, 128, 64) 73792 ['dec4_concat[0][0]'] dec4_conv1_norm (BatchNorm (None, 128, 128, 64) 256 ['dec4_conv1_conv[0][0]'] alization) dec4_conv1_acti (Activatio (None, 128, 128, 64) 0 ['dec4_conv1_norm[0][0]'] n) dec4_conv2_conv (Conv2D) (None, 128, 128, 64) 36928 ['dec4_conv1_acti[0][0]'] dec4_conv2_norm (BatchNorm (None, 128, 128, 64) 256 ['dec4_conv2_conv[0][0]'] alization) dec4_conv2_acti (Activatio (None, 128, 128, 64) 0 ['dec4_conv2_norm[0][0]'] n) outputs_conv (Conv2D) (None, 128, 128, 1) 65 ['dec4_conv2_acti[0][0]'] outputs_norm (BatchNormali (None, 128, 128, 1) 4 ['outputs_conv[0][0]'] zation) outputs_acti (Activation) (None, 128, 128, 1) 0 ['outputs_norm[0][0]'] ================================================================================================== Total params: 31055301 (118.47 MB) Trainable params: 31043523 (118.42 MB) Non-trainable params: 11778 (46.01 KB) __________________________________________________________________________________________________
Trénování modelu
Dostávám se k samotnému procesu trénování modelu na datové sadě.
Opět si data rozdělím na podmnožinu pro trénování a pro validaci. Navíc mám vydefinované dvě callback funkce. Jedna je pro ukončení trénování v okamžiku, kdy by se mně výkon modelu na validační sadě začne zhoršovat. A ta druhá funkce je pro uložení modelu s aktuálně nejlepšími výsledky.
Počet epoch pro trénování je nastaven na 100 a jak uvidíte z následujícího průběhu, je také plně využit (výpis jsem pro přehlednost trochu zkrátil).
In [11]:
MODEL_CHECKPOINT = f"/kaggle/working/model/{model.name}.ckpt"
EPOCHS = 100
callbacks_list = [
keras.callbacks.EarlyStopping(monitor='val_dsc', mode='max', patience=20),
keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_dsc', save_best_only=True, mode='max', verbose=1)
]
history = model.fit(
x=x_train,
y=y_train,
epochs=EPOCHS,
callbacks=callbacks_list,
validation_split=0.2,
verbose=1)
Epoch 1/100
79/79 [==============================] - ETA: 0s - loss: 1.6389 - accuracy: 0.8555 - dsc: 0.0315
Epoch 1: val_dsc improved from -inf to 0.02355, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 47s 411ms/step - loss: 1.6389 - accuracy: 0.8555 - dsc: 0.0315 - val_loss: 4.4048 - val_accuracy: 0.0234 - val_dsc: 0.0236
Epoch 2/100
79/79 [==============================] - ETA: 0s - loss: 1.5849 - accuracy: 0.9585 - dsc: 0.0339
Epoch 2: val_dsc improved from 0.02355 to 0.02769, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 394ms/step - loss: 1.5849 - accuracy: 0.9585 - dsc: 0.0339 - val_loss: 1.8415 - val_accuracy: 0.3880 - val_dsc: 0.0277
Epoch 3/100
79/79 [==============================] - ETA: 0s - loss: 1.5417 - accuracy: 0.9740 - dsc: 0.0368
Epoch 3: val_dsc improved from 0.02769 to 0.03993, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 392ms/step - loss: 1.5417 - accuracy: 0.9740 - dsc: 0.0368 - val_loss: 1.6092 - val_accuracy: 0.9535 - val_dsc: 0.0399
Epoch 4/100
79/79 [==============================] - ETA: 0s - loss: 1.5041 - accuracy: 0.9817 - dsc: 0.0390
Epoch 4: val_dsc did not improve from 0.03993
79/79 [==============================] - 21s 272ms/step - loss: 1.5041 - accuracy: 0.9817 - dsc: 0.0390 - val_loss: 1.5018 - val_accuracy: 0.9863 - val_dsc: 0.0348
Epoch 5/100
79/79 [==============================] - ETA: 0s - loss: 1.4712 - accuracy: 0.9844 - dsc: 0.0403
Epoch 5: val_dsc improved from 0.03993 to 0.04579, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 395ms/step - loss: 1.4712 - accuracy: 0.9844 - dsc: 0.0403 - val_loss: 1.4427 - val_accuracy: 0.9822 - val_dsc: 0.0458
Epoch 6/100
79/79 [==============================] - ETA: 0s - loss: 1.4394 - accuracy: 0.9866 - dsc: 0.0422
Epoch 6: val_dsc improved from 0.04579 to 0.05077, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 395ms/step - loss: 1.4394 - accuracy: 0.9866 - dsc: 0.0422 - val_loss: 1.4176 - val_accuracy: 0.9812 - val_dsc: 0.0508
Epoch 7/100
79/79 [==============================] - ETA: 0s - loss: 1.4089 - accuracy: 0.9879 - dsc: 0.0448
Epoch 7: val_dsc improved from 0.05077 to 0.05292, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 394ms/step - loss: 1.4089 - accuracy: 0.9879 - dsc: 0.0448 - val_loss: 1.3859 - val_accuracy: 0.9890 - val_dsc: 0.0529
Epoch 8/100
79/79 [==============================] - ETA: 0s - loss: 1.3816 - accuracy: 0.9889 - dsc: 0.0470
Epoch 8: val_dsc did not improve from 0.05292
79/79 [==============================] - 21s 272ms/step - loss: 1.3816 - accuracy: 0.9889 - dsc: 0.0470 - val_loss: 1.4646 - val_accuracy: 0.9305 - val_dsc: 0.0515
Epoch 9/100
79/79 [==============================] - ETA: 0s - loss: 1.3530 - accuracy: 0.9897 - dsc: 0.0498
Epoch 9: val_dsc improved from 0.05292 to 0.05989, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 393ms/step - loss: 1.3530 - accuracy: 0.9897 - dsc: 0.0498 - val_loss: 1.3038 - val_accuracy: 0.9912 - val_dsc: 0.0599
Epoch 10/100
79/79 [==============================] - ETA: 0s - loss: 1.3289 - accuracy: 0.9900 - dsc: 0.0525
Epoch 10: val_dsc did not improve from 0.05989
79/79 [==============================] - 21s 272ms/step - loss: 1.3289 - accuracy: 0.9900 - dsc: 0.0525 - val_loss: 1.3039 - val_accuracy: 0.9875 - val_dsc: 0.0566
...
Epoch 90/100
79/79 [==============================] - ETA: 0s - loss: 0.1536 - accuracy: 0.9980 - dsc: 0.8563
Epoch 90: val_dsc improved from 0.83179 to 0.83274, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 30s 388ms/step - loss: 0.1536 - accuracy: 0.9980 - dsc: 0.8563 - val_loss: 0.1841 - val_accuracy: 0.9970 - val_dsc: 0.8327
Epoch 91/100
79/79 [==============================] - ETA: 0s - loss: 0.1461 - accuracy: 0.9981 - dsc: 0.8629
Epoch 91: val_dsc improved from 0.83274 to 0.83919, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 30s 388ms/step - loss: 0.1461 - accuracy: 0.9981 - dsc: 0.8629 - val_loss: 0.1788 - val_accuracy: 0.9970 - val_dsc: 0.8392
Epoch 92/100
79/79 [==============================] - ETA: 0s - loss: 0.1459 - accuracy: 0.9981 - dsc: 0.8633
Epoch 92: val_dsc did not improve from 0.83919
79/79 [==============================] - 21s 269ms/step - loss: 0.1459 - accuracy: 0.9981 - dsc: 0.8633 - val_loss: 0.1787 - val_accuracy: 0.9970 - val_dsc: 0.8366
Epoch 93/100
79/79 [==============================] - ETA: 0s - loss: 0.1442 - accuracy: 0.9981 - dsc: 0.8647
Epoch 93: val_dsc did not improve from 0.83919
79/79 [==============================] - 21s 269ms/step - loss: 0.1442 - accuracy: 0.9981 - dsc: 0.8647 - val_loss: 0.1795 - val_accuracy: 0.9969 - val_dsc: 0.8357
Epoch 94/100
79/79 [==============================] - ETA: 0s - loss: 0.1348 - accuracy: 0.9981 - dsc: 0.8738
Epoch 94: val_dsc improved from 0.83919 to 0.84365, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 31s 389ms/step - loss: 0.1348 - accuracy: 0.9981 - dsc: 0.8738 - val_loss: 0.1728 - val_accuracy: 0.9970 - val_dsc: 0.8436
Epoch 95/100
79/79 [==============================] - ETA: 0s - loss: 0.1419 - accuracy: 0.9980 - dsc: 0.8675
Epoch 95: val_dsc did not improve from 0.84365
79/79 [==============================] - 21s 269ms/step - loss: 0.1419 - accuracy: 0.9980 - dsc: 0.8675 - val_loss: 0.1901 - val_accuracy: 0.9966 - val_dsc: 0.8284
Epoch 96/100
79/79 [==============================] - ETA: 0s - loss: 0.1371 - accuracy: 0.9980 - dsc: 0.8715
Epoch 96: val_dsc improved from 0.84365 to 0.85173, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 30s 387ms/step - loss: 0.1371 - accuracy: 0.9980 - dsc: 0.8715 - val_loss: 0.1646 - val_accuracy: 0.9970 - val_dsc: 0.8517
Epoch 97/100
79/79 [==============================] - ETA: 0s - loss: 0.1290 - accuracy: 0.9981 - dsc: 0.8777
Epoch 97: val_dsc improved from 0.85173 to 0.85611, saving model to /kaggle/working/model/UNet.ckpt
79/79 [==============================] - 30s 387ms/step - loss: 0.1290 - accuracy: 0.9981 - dsc: 0.8777 - val_loss: 0.1618 - val_accuracy: 0.9970 - val_dsc: 0.8561
Epoch 98/100
79/79 [==============================] - ETA: 0s - loss: 0.1332 - accuracy: 0.9980 - dsc: 0.8754
Epoch 98: val_dsc did not improve from 0.85611
79/79 [==============================] - 21s 269ms/step - loss: 0.1332 - accuracy: 0.9980 - dsc: 0.8754 - val_loss: 0.2616 - val_accuracy: 0.9955 - val_dsc: 0.7949
Epoch 99/100
79/79 [==============================] - ETA: 0s - loss: 0.1888 - accuracy: 0.9971 - dsc: 0.8289
Epoch 99: val_dsc did not improve from 0.85611
79/79 [==============================] - 21s 269ms/step - loss: 0.1888 - accuracy: 0.9971 - dsc: 0.8289 - val_loss: 0.1879 - val_accuracy: 0.9966 - val_dsc: 0.8351
Epoch 100/100
79/79 [==============================] - ETA: 0s - loss: 0.1401 - accuracy: 0.9978 - dsc: 0.8699
Epoch 100: val_dsc did not improve from 0.85611
79/79 [==============================] - 21s 269ms/step - loss: 0.1401 - accuracy: 0.9978 - dsc: 0.8699 - val_loss: 0.1697 - val_accuracy: 0.9968 - val_dsc: 0.8462
A takto vypadal průběh trénování graficky. Na levé straně je zobrazen vývoj ztrátové funkce, na pravé straně pak metriky:
In [12]:
fig, ax = plt.subplots(1, 2, figsize=(16, 4)) sns.lineplot(data={k: history.history[k] for k in ('loss', 'val_loss')}, ax=ax[0]) sns.lineplot(data={k: history.history[k] for k in history.history.keys() if k not in ('loss', 'val_loss')}, ax=ax[1]) plt.show()
Nyní si zpětně načtu váhy modelu s nejlepšími výsledky na validační sadě. Na tomto modelu budu dělat ověření výsledku na testovací sadě.
In [13]:
model.load_weights(f"/kaggle/working/model/{model.name}.ckpt")
Out[13]:
<tensorflow.python.checkpoint.checkpoint.CheckpointLoadStatus at 0x7e44882a4c10>
Ověření výsledků modelu
Nejdříve si udělám predikci pro celou testovací sadu.
Jen pro připomenutí, výsledkem predikce je opět obrázek se stejným rozlišení, jako byl ten původní. Rozdíl tady ale je. Hodnotou každého pixelu je pravděpodobnost, s jakou bod odpovídá nádoru. Pro vyhodnocení si tedy za pozitivní vezmu pouze ty body, které mají pravděpodobnost větší jak 0.5.
In [14]:
y_pred = model.predict(x_test) y_pred = (y_pred > 0.5).astype(np.float64) 25/25 [==============================] - 3s 98ms/step
A nyní si několik vzorků zobrazím, abych měl nějakou představu o výsledků (vybral jsem jen ty vzorky s nádorem, v testovací sadě jsou pochopitelně i vzorky, kde žádné nádory nejsou).
In [15]:
for _ in range(20):
i = np.random.randint(len(y_test))
if y_test[i].sum() > 0:
plt.figure(figsize=(8, 8))
plt.subplot(1,3,1)
plt.imshow(x_test[i])
plt.title('Original Image')
plt.subplot(1,3,2)
plt.imshow(y_test[i])
plt.title('Original Mask')
plt.subplot(1,3,3)
plt.imshow(y_pred[i])
plt.title('Prediction')
plt.show()
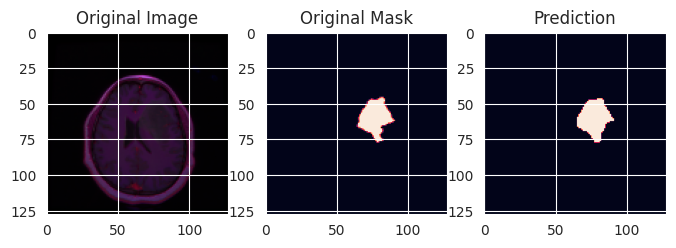
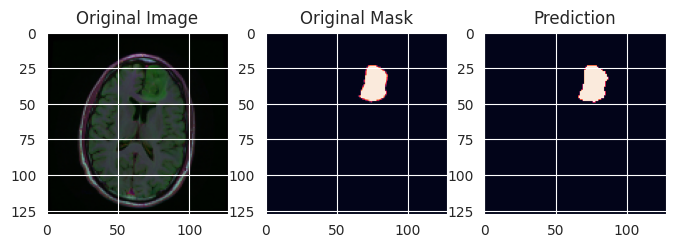
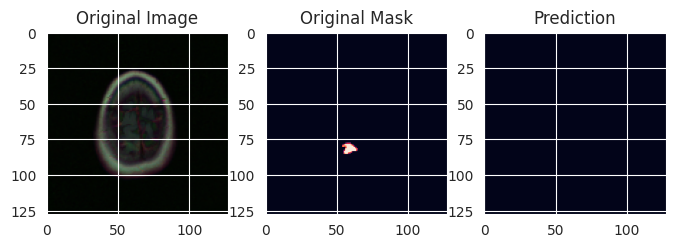
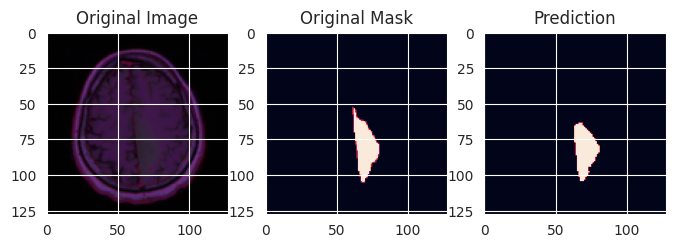
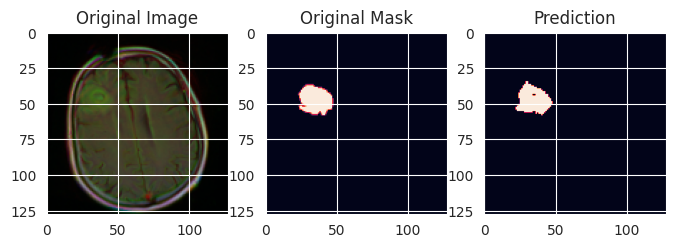
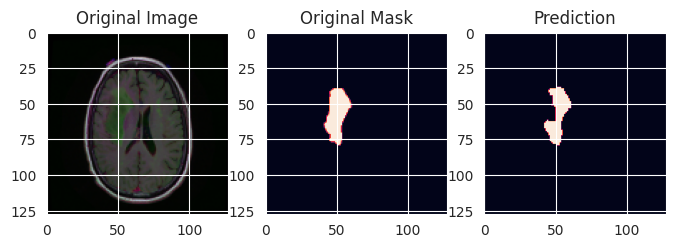
Jako ukázka je to dobré, ale chtělo by to ještě poněkud lepší vyhodnocení.
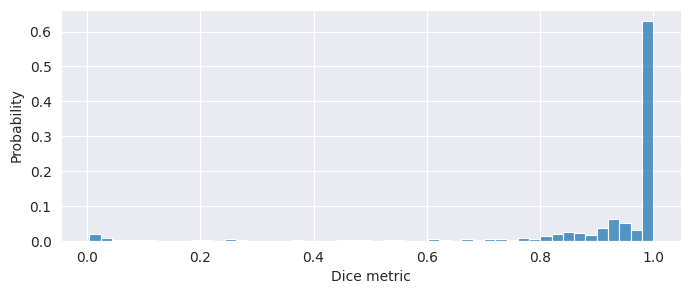
Spočítám si Dice Coefficient pro každý vzorek z testovací sady a udělám si z výsledků histogram:
In [16]:
pred_dice_metric = np.array([dsc(y_test[i], y_pred[i]).numpy() for i in range(len(y_test))])
In [17]:
fig=plt.figure(figsize=(8, 3)) sns.histplot(pred_dice_metric, stat="probability", bins=50) plt.xlabel("Dice metric") plt.show()
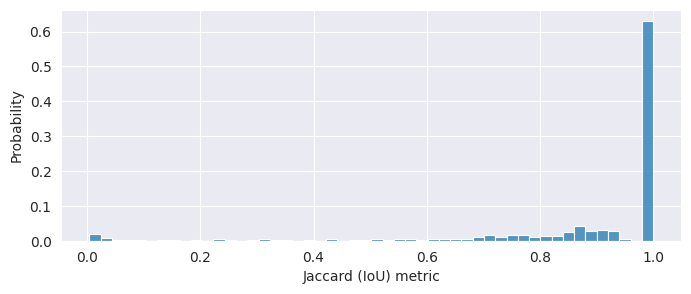
A totéž pro srovnání ještě Jaccard Index:
In [18]:
pred_jaccard_metric = np.array([jaccard_similarity(y_test[i], y_pred[i]).numpy() for i in range(len(y_test))])
In [19]:
fig=plt.figure(figsize=(8, 3)) sns.histplot(pred_jaccard_metric, stat="probability", bins=50) plt.xlabel("Jaccard (IoU) metric") plt.show()
Žádné názory
ČLÁNKY DO MAILU