Klasifikace Elektrokardiogramu (EKG) - díl druhý
2. 2. 2024 0:00
Jiří Raška
Tento článek navazuje na předchozí: Klasifikace Elektrokardiogramu (EKG) – díl první.
Modelování samostatných datových sad
Co ode mně můžete v této kapitole očekávat?
Nejdříve se budu zabývat modely pro každou vstupní sadu (X, Y a S) samostatně. V případě datové sady X to budou plně propojené neuronové vrstvy. U datové sady Y, jak již vyplývá z podstaty EKG křivek, to budou 1D konvoluční sítě. No a v případě datové sady S pak oddělené 2D konvoluční vrstvy pro každý svod zvláště.
Dále se pak pokusím propojit tyto modely dohromady s cílem zlepšení celkových výsledků klasifikačního modelu.
Dříve, než se pustím do samostatných modelů, potřebuji si připravit nějaké funkce pro vyhodnocování výsledků:
In [19]:
def model_quality_reporting(test, pred, *, model_name='model', labels=("NORM", "MI", "STTC", "CD", "HYP")):
def print_confusion_matrix(confusion_matrix, axes, class_label, class_names, fontsize=14):
df_cm = pd.DataFrame(confusion_matrix, index=class_names, columns=class_names)
try:
heatmap = sns.heatmap(df_cm, annot=True, fmt="d", cbar=False, ax=axes)
except ValueError:
raise ValueError("Confusion matrix values must be integers.")
heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation=0, ha='right', fontsize=fontsize)
heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation=45, ha='right', fontsize=fontsize)
axes.set_ylabel('True label')
axes.set_xlabel('Predicted label')
axes.set_title("Class - " + class_label)
fig, ax = plt.subplots(1, 5, figsize=(16, 3))
for axes, cfs_matrix, label in zip(ax.flatten(), sklearn.metrics.multilabel_confusion_matrix(test, pred), labels):
print_confusion_matrix(cfs_matrix, axes, label, ["N", "Y"])
fig.tight_layout()
plt.show()
print(sklearn.metrics.classification_report(test, pred, target_names=labels, zero_division=0))
m = sklearn.metrics.classification_report(test, pred, target_names=labels, output_dict=True, zero_division=False)
m = {(model_name, k): m[k] for k in labels}
return pd.DataFrame.from_dict(m, orient='index')
metrics = pd.DataFrame(columns=("precision", "recall", "f1-score", "support"), index=pd.MultiIndex.from_tuples([], names=('model', 'group')))
Funkcemodel_quality_report mně zajisti vykreslení tzv. confusion matrix (do překladu se pouštět nebudu). Dále bude vypsána také detailní klasifikační zpráva, kde mne budou zajímat především metriky Precision, Recall a F1-score pro všechny klasifikační třídy. No a klasifikační zpráva je také návratovou hodnotou funkce, což budu používat pro jejich uschování a finální porovnání výkonu jednotlivých modelů. Celkové výsledky se budou agregovat v proměnné metrics .
Referenční model
Ten jsem v úvodu nezmiňoval, ale vždy je dobré si nějaký udělat. Budu mít alespoň odrazový můstek pro porovnání, zda se mé modely skutečně něco naučily.
Za referenční model použiji náhodně generované třídy s pravděpodobností odpovídající zastoupení tříd v trénovací sadě Z_train .
In [20]:
Z_prob = Z_train.sum(axis=0) / Z_train.shape[0] Z_pred = np.random.uniform(size=Z_test.shape) for i in range(Z_pred.shape[-1]): Z_pred[:, i] = (Z_pred[:, i] < Z_prob[i]).astype('float64')
A nyní vyhodnocení takového modelu:
In [21]:
metrics = pd.concat([metrics.drop('REF_model', level=0, errors='ignore'), model_quality_reporting(Z_test, Z_pred, model_name='REF_model')])
precision recall f1-score support
NORM 0.45 0.45 0.45 964
MI 0.26 0.27 0.27 553
STTC 0.23 0.23 0.23 523
CD 0.20 0.20 0.20 498
HYP 0.15 0.13 0.14 263
micro avg 0.30 0.30 0.30 2801
macro avg 0.26 0.26 0.26 2801
weighted avg 0.30 0.30 0.30 2801
samples avg 0.24 0.32 0.25 2801
Z váše uvedeného je zřejmé, že model moc úspěšný v rozpoznávání není.
X model – pro metadata
Připravím si funkci pro generování modelu datové sady X:
In [22]:
def create_X_model(X, *, units=32, dropouts=0.3):
X = keras.layers.Normalization(axis=-1, name='X_norm')(X)
X = keras.layers.Dense(units, activation='relu', name='X_dense_1')(X)
X = keras.layers.Dropout(dropouts, name='X_drop_1')(X)
X = keras.layers.Dense(units, activation='relu', name='X_dense_2')(X)
X = keras.layers.Dropout(dropouts, name='X_drop_2')(X)
return X
Funkce vytvoří dvě plně propojené vrstvy s aktivační funkcí RELU. Doplnil jsem ještě dvě vrstvyDropout pro potlačení problému se zmenšováním gradientu (gradient descent). Toto vše ale předchází ještě jedna vrstva Normalization , která zajistí normalizaci vstupních dat podle poslední osy v datovém setu.
In [23]:
def create_model01(X_shape, Z_shape):
X_inputs = keras.Input(X_shape[1:], name='X_inputs')
X = create_X_model(X_inputs, units=64)
X = keras.layers.Dense(64, activation='relu', name='Z_dense_1')(X)
X = keras.layers.Dense(64, activation='relu', name='Z_dense_2')(X)
X = keras.layers.Dropout(0.5, name='Z_drop_1')(X)
outputs = keras.layers.Dense(Z_shape[-1], activation='sigmoid', name='Z_outputs')(X)
model = keras.Model(inputs=X_inputs, outputs=outputs, name='X_model')
return model
Celý model pak vytvořím tak, že zavolám funkcicreate_X_model a doplním výsledek o další dvě plně propojené vrstvy včetně regulace. Výstupem je pak poslední vrstva, která má počet neuronů shodný s počtem klasifikačních tříd (v mém případě je to 5). Aktivační funkcí je v tomto případě Sigmoid , takže výsledkem bude pravděpodobnost zařazení vzorku do dané skupiny (jen připomínám, že vzorek může být zařazen do více jak jedné skupiny).
Nyní již můžu model přeložit.
Za zmínku ještě stojí použití binární entropie jako loss function, tedy to, co budu optimalizovat. Jako sledované metriky budu pro trénování používat binary
accuracy ,precision a recall .
In [24]:
model01 = create_model01(X_train.shape, Z_train.shape) model01.compile(optimizer='adam', loss='binary_crossentropy', metrics=['binary_accuracy', 'Precision', 'Recall']) model01.summary() Model: "X_model" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= X_inputs (InputLayer) [(None, 7)] 0 X_norm (Normalization) (None, 7) 15 X_dense_1 (Dense) (None, 64) 512 X_drop_1 (Dropout) (None, 64) 0 X_dense_2 (Dense) (None, 64) 4160 X_drop_2 (Dropout) (None, 64) 0 Z_dense_1 (Dense) (None, 64) 4160 Z_dense_2 (Dense) (None, 64) 4160 Z_drop_1 (Dropout) (None, 64) 0 Z_outputs (Dense) (None, 5) 325 ================================================================= Total params: 13332 (52.08 KB) Trainable params: 13317 (52.02 KB) Non-trainable params: 15 (64.00 Byte) _________________________________________________________________
Pro trénování budu používat early stopping, což mně zajistí zastavení trénování v okamžiku, kdy se mně začnou zhoršovat výsledky loss function na validační sadě. Váhy modelu s nejlepšími výsledky si budu průběžně schovávat do souboru tak, bych si je mohl po trénování zpětně načíst.
In [25]:
MODEL_CHECKPOINT = '/kaggle/working/model/model01.ckpt' callbacks_list = [ keras.callbacks.EarlyStopping(monitor='val_binary_accuracy', patience=10), keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_binary_accuracy', save_best_only=True) ] history = model01.fit(X_train, Z_train, epochs=40, batch_size=32, callbacks=callbacks_list, validation_data=(X_valid, Z_valid)) model01 = keras.models.load_model(MODEL_CHECKPOINT) model01.save('/kaggle/working/model/model01.keras') Epoch 1/40 546/546 [==============================] - 10s 8ms/step - loss: 0.6957 - binary_accuracy: 0.7139 - precision: 0.3742 - recall: 0.1823 - val_loss: 0.5378 - val_binary_accuracy: 0.7691 - val_precision: 0.6978 - val_recall: 0.1705 Epoch 2/40 546/546 [==============================] - 3s 5ms/step - loss: 0.5456 - binary_accuracy: 0.7556 - precision: 0.6127 - recall: 0.1110 - val_loss: 0.5235 - val_binary_accuracy: 0.7668 - val_precision: 0.7261 - val_recall: 0.1409 Epoch 3/40 546/546 [==============================] - 3s 5ms/step - loss: 0.5307 - binary_accuracy: 0.7616 - precision: 0.6862 - recall: 0.1188 - val_loss: 0.5134 - val_binary_accuracy: 0.7689 - val_precision: 0.6845 - val_recall: 0.1780 Epoch 4/40 546/546 [==============================] - 4s 7ms/step - loss: 0.5200 - binary_accuracy: 0.7673 - precision: 0.7002 - recall: 0.1521 - val_loss: 0.5083 - val_binary_accuracy: 0.7788 - val_precision: 0.7194 - val_recall: 0.2205 Epoch 5/40 546/546 [==============================] - 4s 7ms/step - loss: 0.5092 - binary_accuracy: 0.7729 - precision: 0.7198 - recall: 0.1779 - val_loss: 0.4921 - val_binary_accuracy: 0.7808 - val_precision: 0.7412 - val_recall: 0.2187 Epoch 6/40 546/546 [==============================] - 4s 7ms/step - loss: 0.4979 - binary_accuracy: 0.7786 - precision: 0.7283 - recall: 0.2092 - val_loss: 0.4868 - val_binary_accuracy: 0.7874 - val_precision: 0.7511 - val_recall: 0.2519 Epoch 7/40 546/546 [==============================] - 4s 8ms/step - loss: 0.4883 - binary_accuracy: 0.7837 - precision: 0.7276 - recall: 0.2418 - val_loss: 0.4808 - val_binary_accuracy: 0.7919 - val_precision: 0.7225 - val_recall: 0.3018 Epoch 8/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4826 - binary_accuracy: 0.7880 - precision: 0.7391 - recall: 0.2600 - val_loss: 0.4768 - val_binary_accuracy: 0.7915 - val_precision: 0.7258 - val_recall: 0.2965 Epoch 9/40 546/546 [==============================] - 4s 7ms/step - loss: 0.4808 - binary_accuracy: 0.7886 - precision: 0.7424 - recall: 0.2610 - val_loss: 0.4764 - val_binary_accuracy: 0.7921 - val_precision: 0.7280 - val_recall: 0.2979 Epoch 10/40 546/546 [==============================] - 4s 7ms/step - loss: 0.4798 - binary_accuracy: 0.7888 - precision: 0.7503 - recall: 0.2565 - val_loss: 0.4772 - val_binary_accuracy: 0.7929 - val_precision: 0.7445 - val_recall: 0.2890 Epoch 11/40 546/546 [==============================] - 4s 7ms/step - loss: 0.4782 - binary_accuracy: 0.7902 - precision: 0.7456 - recall: 0.2683 - val_loss: 0.4735 - val_binary_accuracy: 0.7937 - val_precision: 0.7422 - val_recall: 0.2958 Epoch 12/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4769 - binary_accuracy: 0.7905 - precision: 0.7545 - recall: 0.2638 - val_loss: 0.4784 - val_binary_accuracy: 0.7882 - val_precision: 0.6823 - val_recall: 0.3211 Epoch 13/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4762 - binary_accuracy: 0.7909 - precision: 0.7542 - recall: 0.2664 - val_loss: 0.4739 - val_binary_accuracy: 0.7920 - val_precision: 0.7186 - val_recall: 0.3061 Epoch 14/40 546/546 [==============================] - 4s 7ms/step - loss: 0.4747 - binary_accuracy: 0.7910 - precision: 0.7520 - recall: 0.2680 - val_loss: 0.4722 - val_binary_accuracy: 0.7939 - val_precision: 0.7512 - val_recall: 0.2897 Epoch 15/40 546/546 [==============================] - 4s 7ms/step - loss: 0.4735 - binary_accuracy: 0.7911 - precision: 0.7537 - recall: 0.2679 - val_loss: 0.4720 - val_binary_accuracy: 0.7944 - val_precision: 0.7577 - val_recall: 0.2879 Epoch 16/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4731 - binary_accuracy: 0.7917 - precision: 0.7621 - recall: 0.2655 - val_loss: 0.4733 - val_binary_accuracy: 0.7907 - val_precision: 0.7089 - val_recall: 0.3075 Epoch 17/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4726 - binary_accuracy: 0.7923 - precision: 0.7671 - recall: 0.2654 - val_loss: 0.4723 - val_binary_accuracy: 0.7940 - val_precision: 0.7491 - val_recall: 0.2918 Epoch 18/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4729 - binary_accuracy: 0.7917 - precision: 0.7614 - recall: 0.2661 - val_loss: 0.4747 - val_binary_accuracy: 0.7940 - val_precision: 0.7641 - val_recall: 0.2808 Epoch 19/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4722 - binary_accuracy: 0.7923 - precision: 0.7646 - recall: 0.2673 - val_loss: 0.4708 - val_binary_accuracy: 0.7918 - val_precision: 0.7230 - val_recall: 0.3007 Epoch 20/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4709 - binary_accuracy: 0.7922 - precision: 0.7685 - recall: 0.2640 - val_loss: 0.4731 - val_binary_accuracy: 0.7920 - val_precision: 0.7208 - val_recall: 0.3040 Epoch 21/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4719 - binary_accuracy: 0.7920 - precision: 0.7659 - recall: 0.2648 - val_loss: 0.4694 - val_binary_accuracy: 0.7934 - val_precision: 0.7441 - val_recall: 0.2925 Epoch 22/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4727 - binary_accuracy: 0.7918 - precision: 0.7676 - recall: 0.2626 - val_loss: 0.4697 - val_binary_accuracy: 0.7927 - val_precision: 0.7413 - val_recall: 0.2904 Epoch 23/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4719 - binary_accuracy: 0.7917 - precision: 0.7592 - recall: 0.2677 - val_loss: 0.4730 - val_binary_accuracy: 0.7937 - val_precision: 0.7379 - val_recall: 0.2993 Epoch 24/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4705 - binary_accuracy: 0.7920 - precision: 0.7622 - recall: 0.2668 - val_loss: 0.4693 - val_binary_accuracy: 0.7936 - val_precision: 0.7533 - val_recall: 0.2865 Epoch 25/40 546/546 [==============================] - 3s 5ms/step - loss: 0.4703 - binary_accuracy: 0.7924 - precision: 0.7683 - recall: 0.2655 - val_loss: 0.4697 - val_binary_accuracy: 0.7938 - val_precision: 0.7576 - val_recall: 0.2843
A nyní si můžu zobrazit průběh trénování:
In [26]:
sns.relplot(data=pd.DataFrame(history.history), kind='line', height=4, aspect=4)
plt.show()
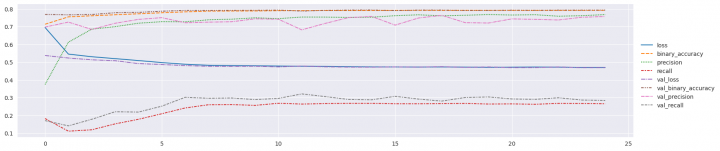
Posledním krokem v této části bude vytvoření predikce z testovací sady a její detailní vyhodnocení:
In [27]:
Z_pred = np.around(model01.predict(X_test, verbose=0))
metrics = pd.concat([metrics.drop(model01.name, level=0, errors='ignore'), model_quality_reporting(Z_test, Z_pred, model_name=model01.name)])
precision recall f1-score support
NORM 0.71 0.57 0.64 964
MI 0.97 0.40 0.56 553
STTC 0.00 0.00 0.00 523
CD 0.00 0.00 0.00 498
HYP 0.00 0.00 0.00 263
micro avg 0.77 0.28 0.41 2801
macro avg 0.34 0.19 0.24 2801
weighted avg 0.44 0.28 0.33 2801
samples avg 0.35 0.32 0.33 2801
Z výsledku je zřejmé, že model je schopen podchytit pouze nejčastěji zastoupené třídy v datech. Ostatní pak není schopen zachytit vůbec.
Y model – pro EKG křivky
Opět připravím funkci, která mně vytvoří model specifický pro datovou sadu Y:
In [28]:
def create_Y_model(X, *, filters=(32, 64, 128), kernel_size=(5, 3, 3), strides=(1, 1, 1)):
f1, f2, f3 = filters
k1, k2, k3 = kernel_size
s1, s2, s3 = strides
X = keras.layers.Normalization(axis=-1, name='Y_norm')(X)
X = keras.layers.Conv1D(f1, k1, strides=s1, padding='same', name='Y_conv_1')(X)
X = keras.layers.BatchNormalization(name='Y_norm_1')(X)
X = keras.layers.ReLU(name='Y_relu_1')(X)
X = keras.layers.MaxPool1D(2, name='Y_pool_1')(X)
X = keras.layers.Conv1D(f2, k2, strides=s2, padding='same', name='Y_conv_2')(X)
X = keras.layers.BatchNormalization(name='Y_norm_2')(X)
X = keras.layers.ReLU(name='Y_relu_2')(X)
X = keras.layers.MaxPool1D(2, name='Y_pool_2')(X)
X = keras.layers.Conv1D(f3, k3, strides=s3, padding='same', name='Y_conv_3')(X)
X = keras.layers.BatchNormalization(name='Y_norm_3')(X)
X = keras.layers.ReLU(name='Y_relu_3')(X)
X = keras.layers.GlobalAveragePooling1D(name='Y_aver')(X)
X = keras.layers.Dropout(0.5, name='Y_drop')(X)
return X
Funkce obsahuje tři samostatné bloky pro 1D konvoluční vrstvy. V parametrech funkce se zadávají hodnoty pro počet filtrů, velikost kernelu a krok každé vrstvy. V každé vrstvě se následně provede normalizace a doplní aktivační funkce RELU.
Konvoluční vrstvy jsou proloženy agregačními vrstvami MaxPool1D , které zajišťují redukci v časové ose na polovinu.
Poslední vrstvou je GlobalAveragePooling1D , která provede úplné potlačení časové dimenze, a zůstane pouze dimenze vlastností (features).
Všechny výše uvedené vrstvy předchází ještě jedna vrstva určená pro normalizaci vstupních dat, tedy vrstva Normalization .
To, jak se dimenze na jednotlivých vrstvách transformují, bude asi lépe vidět na výpisu modelu po překladu. Což bude o dva kroky dále.
A nyní ještě funkce pro vytvoření celého modelu:
In [29]:
def create_model02(Y_shape, Z_shape):
Y_inputs = keras.Input(Y_shape[1:], name='Y_inputs')
X = create_Y_model(Y_inputs, filters=(64, 128, 256), kernel_size=(7, 3, 3))
X = keras.layers.Dense(128, activation='relu', name='Z_dense_1')(X)
X = keras.layers.Dense(128, activation='relu', name='Z_dense_2')(X)
X = keras.layers.Dropout(0.5, name='Z_drop_1')(X)
outputs = keras.layers.Dense(Z_shape[-1], activation='sigmoid', name='Z_outputs')(X)
model = keras.Model(inputs=Y_inputs, outputs=outputs, name='Y_model')
return model
Princip je stejný jak tomu bylo u předchozího modelu, proto jen nějaké poznámky:
-
počty filtrů pro konvoluční vrstvy jsem použil 64, 128 a 256
-
velikosti kernelů pak 7 pro první vrstvu a 3 pro další dvě
-
krok zůstal u všech vrstev stejný, tedy 1
No a nyní tedy překlad modelu:
In [30]:
model02 = create_model02(Y_train.shape, Z_train.shape) model02.compile(optimizer='adam', loss='binary_crossentropy', metrics=['binary_accuracy', 'Precision', 'Recall']) model02.summary() Model: "Y_model" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= Y_inputs (InputLayer) [(None, 1000, 12)] 0 Y_norm (Normalization) (None, 1000, 12) 25 Y_conv_1 (Conv1D) (None, 1000, 64) 5440 Y_norm_1 (BatchNormalizati (None, 1000, 64) 256 on) Y_relu_1 (ReLU) (None, 1000, 64) 0 Y_pool_1 (MaxPooling1D) (None, 500, 64) 0 Y_conv_2 (Conv1D) (None, 500, 128) 24704 Y_norm_2 (BatchNormalizati (None, 500, 128) 512 on) Y_relu_2 (ReLU) (None, 500, 128) 0 Y_pool_2 (MaxPooling1D) (None, 250, 128) 0 Y_conv_3 (Conv1D) (None, 250, 256) 98560 Y_norm_3 (BatchNormalizati (None, 250, 256) 1024 on) Y_relu_3 (ReLU) (None, 250, 256) 0 Y_aver (GlobalAveragePooli (None, 256) 0 ng1D) Y_drop (Dropout) (None, 256) 0 Z_dense_1 (Dense) (None, 128) 32896 Z_dense_2 (Dense) (None, 128) 16512 Z_drop_1 (Dropout) (None, 128) 0 Z_outputs (Dense) (None, 5) 645 ================================================================= Total params: 180574 (705.37 KB) Trainable params: 179653 (701.77 KB) Non-trainable params: 921 (3.60 KB) _________________________________________________________________
Ve výpisu je vidět, jak se poslední dimenze ze vstupních dat (12 svodů) postupně mění na 64, 128 a 256 features. Současně je také vidět redukce časové dimenze (to je ta druhá) z původních 1000 na 500 a 250 prostřednictvím vrstvy MaxPooling1D. Až nakonec úplné potlačení časové dimenze s využitím GlobalAveragePooling1D.
Výstupem modelu je opět 5 pravděpodobností pro každou klasifikační třídu.
Můžu tedy přistoupit ke trénování:
In [31]:
MODEL_CHECKPOINT = '/kaggle/working/model/model02.ckpt' callbacks_list = [ keras.callbacks.EarlyStopping(monitor='val_binary_accuracy', patience=10), keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_binary_accuracy', save_best_only=True) ] history = model02.fit(Y_train, Z_train, epochs=100, batch_size=32, callbacks=callbacks_list, validation_data=(Y_valid, Z_valid)) model02 = keras.models.load_model(MODEL_CHECKPOINT) model02.save('/kaggle/working/model/model02.keras') Epoch 1/100 546/546 [==============================] - 17s 16ms/step - loss: 0.4157 - binary_accuracy: 0.8152 - precision: 0.6886 - recall: 0.5013 - val_loss: 0.3688 - val_binary_accuracy: 0.8437 - val_precision: 0.7408 - val_recall: 0.5976 Epoch 2/100 546/546 [==============================] - 8s 14ms/step - loss: 0.3537 - binary_accuracy: 0.8499 - precision: 0.7489 - recall: 0.6186 - val_loss: 0.3546 - val_binary_accuracy: 0.8563 - val_precision: 0.7614 - val_recall: 0.6375 Epoch 3/100 546/546 [==============================] - 6s 10ms/step - loss: 0.3339 - binary_accuracy: 0.8613 - precision: 0.7690 - recall: 0.6515 - val_loss: 0.3528 - val_binary_accuracy: 0.8453 - val_precision: 0.7444 - val_recall: 0.6015 Epoch 4/100 546/546 [==============================] - 8s 15ms/step - loss: 0.3215 - binary_accuracy: 0.8685 - precision: 0.7824 - recall: 0.6704 - val_loss: 0.3236 - val_binary_accuracy: 0.8633 - val_precision: 0.7832 - val_recall: 0.6432 Epoch 5/100 546/546 [==============================] - 8s 14ms/step - loss: 0.3106 - binary_accuracy: 0.8721 - precision: 0.7903 - recall: 0.6782 - val_loss: 0.3331 - val_binary_accuracy: 0.8689 - val_precision: 0.7725 - val_recall: 0.6907 Epoch 6/100 546/546 [==============================] - 6s 10ms/step - loss: 0.3061 - binary_accuracy: 0.8750 - precision: 0.7927 - recall: 0.6899 - val_loss: 0.3175 - val_binary_accuracy: 0.8620 - val_precision: 0.7597 - val_recall: 0.6732 Epoch 7/100 546/546 [==============================] - 8s 15ms/step - loss: 0.2968 - binary_accuracy: 0.8795 - precision: 0.8016 - recall: 0.7005 - val_loss: 0.3174 - val_binary_accuracy: 0.8718 - val_precision: 0.7786 - val_recall: 0.6964 Epoch 8/100 546/546 [==============================] - 8s 16ms/step - loss: 0.2917 - binary_accuracy: 0.8821 - precision: 0.8062 - recall: 0.7075 - val_loss: 0.2889 - val_binary_accuracy: 0.8794 - val_precision: 0.8079 - val_recall: 0.6932 Epoch 9/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2880 - binary_accuracy: 0.8827 - precision: 0.8079 - recall: 0.7078 - val_loss: 0.3355 - val_binary_accuracy: 0.8731 - val_precision: 0.7742 - val_recall: 0.7107 Epoch 10/100 546/546 [==============================] - 8s 14ms/step - loss: 0.2834 - binary_accuracy: 0.8851 - precision: 0.8103 - recall: 0.7170 - val_loss: 0.2798 - val_binary_accuracy: 0.8830 - val_precision: 0.8069 - val_recall: 0.7128 Epoch 11/100 546/546 [==============================] - 8s 15ms/step - loss: 0.2783 - binary_accuracy: 0.8876 - precision: 0.8161 - recall: 0.7214 - val_loss: 0.2862 - val_binary_accuracy: 0.8835 - val_precision: 0.8037 - val_recall: 0.7203 Epoch 12/100 546/546 [==============================] - 6s 11ms/step - loss: 0.2773 - binary_accuracy: 0.8882 - precision: 0.8158 - recall: 0.7249 - val_loss: 0.2972 - val_binary_accuracy: 0.8752 - val_precision: 0.7935 - val_recall: 0.6921 Epoch 13/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2752 - binary_accuracy: 0.8896 - precision: 0.8193 - recall: 0.7272 - val_loss: 0.2860 - val_binary_accuracy: 0.8771 - val_precision: 0.7963 - val_recall: 0.6975 Epoch 14/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2698 - binary_accuracy: 0.8911 - precision: 0.8235 - recall: 0.7290 - val_loss: 0.3070 - val_binary_accuracy: 0.8731 - val_precision: 0.7946 - val_recall: 0.6789 Epoch 15/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2693 - binary_accuracy: 0.8918 - precision: 0.8259 - recall: 0.7292 - val_loss: 0.2906 - val_binary_accuracy: 0.8819 - val_precision: 0.8016 - val_recall: 0.7149 Epoch 16/100 546/546 [==============================] - 8s 14ms/step - loss: 0.2658 - binary_accuracy: 0.8926 - precision: 0.8278 - recall: 0.7303 - val_loss: 0.2797 - val_binary_accuracy: 0.8865 - val_precision: 0.8129 - val_recall: 0.7221 Epoch 17/100 546/546 [==============================] - 6s 11ms/step - loss: 0.2632 - binary_accuracy: 0.8933 - precision: 0.8286 - recall: 0.7329 - val_loss: 0.2784 - val_binary_accuracy: 0.8855 - val_precision: 0.8089 - val_recall: 0.7232 Epoch 18/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2631 - binary_accuracy: 0.8946 - precision: 0.8314 - recall: 0.7358 - val_loss: 0.2824 - val_binary_accuracy: 0.8822 - val_precision: 0.8018 - val_recall: 0.7160 Epoch 19/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2608 - binary_accuracy: 0.8958 - precision: 0.8330 - recall: 0.7391 - val_loss: 0.2848 - val_binary_accuracy: 0.8831 - val_precision: 0.7922 - val_recall: 0.7356 Epoch 20/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2571 - binary_accuracy: 0.8959 - precision: 0.8349 - recall: 0.7371 - val_loss: 0.2756 - val_binary_accuracy: 0.8853 - val_precision: 0.8045 - val_recall: 0.7281 Epoch 21/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2572 - binary_accuracy: 0.8969 - precision: 0.8318 - recall: 0.7464 - val_loss: 0.2905 - val_binary_accuracy: 0.8821 - val_precision: 0.8052 - val_recall: 0.7107 Epoch 22/100 546/546 [==============================] - 8s 15ms/step - loss: 0.2544 - binary_accuracy: 0.8984 - precision: 0.8368 - recall: 0.7470 - val_loss: 0.2740 - val_binary_accuracy: 0.8872 - val_precision: 0.8083 - val_recall: 0.7324 Epoch 23/100 546/546 [==============================] - 5s 9ms/step - loss: 0.2523 - binary_accuracy: 0.8983 - precision: 0.8371 - recall: 0.7461 - val_loss: 0.2771 - val_binary_accuracy: 0.8861 - val_precision: 0.7966 - val_recall: 0.7446 Epoch 24/100 546/546 [==============================] - 5s 9ms/step - loss: 0.2516 - binary_accuracy: 0.8992 - precision: 0.8389 - recall: 0.7480 - val_loss: 0.2770 - val_binary_accuracy: 0.8859 - val_precision: 0.8099 - val_recall: 0.7235 Epoch 25/100 546/546 [==============================] - 5s 9ms/step - loss: 0.2488 - binary_accuracy: 0.9002 - precision: 0.8404 - recall: 0.7509 - val_loss: 0.2826 - val_binary_accuracy: 0.8804 - val_precision: 0.8030 - val_recall: 0.7053 Epoch 26/100 546/546 [==============================] - 5s 10ms/step - loss: 0.2475 - binary_accuracy: 0.8999 - precision: 0.8381 - recall: 0.7525 - val_loss: 0.2775 - val_binary_accuracy: 0.8842 - val_precision: 0.7967 - val_recall: 0.7342 Epoch 27/100 546/546 [==============================] - 5s 10ms/step - loss: 0.2467 - binary_accuracy: 0.9014 - precision: 0.8441 - recall: 0.7522 - val_loss: 0.2806 - val_binary_accuracy: 0.8840 - val_precision: 0.8017 - val_recall: 0.7257 Epoch 28/100 546/546 [==============================] - 6s 10ms/step - loss: 0.2447 - binary_accuracy: 0.9019 - precision: 0.8431 - recall: 0.7556 - val_loss: 0.2843 - val_binary_accuracy: 0.8847 - val_precision: 0.8102 - val_recall: 0.7171 Epoch 29/100 546/546 [==============================] - 5s 10ms/step - loss: 0.2421 - binary_accuracy: 0.9028 - precision: 0.8460 - recall: 0.7561 - val_loss: 0.2698 - val_binary_accuracy: 0.8860 - val_precision: 0.8105 - val_recall: 0.7232 Epoch 30/100 546/546 [==============================] - 5s 10ms/step - loss: 0.2420 - binary_accuracy: 0.9019 - precision: 0.8435 - recall: 0.7553 - val_loss: 0.2918 - val_binary_accuracy: 0.8839 - val_precision: 0.8065 - val_recall: 0.7182 Epoch 31/100 546/546 [==============================] - 5s 10ms/step - loss: 0.2408 - binary_accuracy: 0.9037 - precision: 0.8470 - recall: 0.7593 - val_loss: 0.2764 - val_binary_accuracy: 0.8849 - val_precision: 0.7944 - val_recall: 0.7417 Epoch 32/100 546/546 [==============================] - 5s 10ms/step - loss: 0.2413 - binary_accuracy: 0.9039 - precision: 0.8490 - recall: 0.7574 - val_loss: 0.2796 - val_binary_accuracy: 0.8853 - val_precision: 0.7929 - val_recall: 0.7460
Takto vypadal průběh trénování z pohledu optimalizované funkce a metrik, a to jak pro trénovací tak validační sadu:
In [32]:
sns.relplot(data=pd.DataFrame(history.history), kind='line', height=4, aspect=4)
plt.show()
Nyní již můžu vyhodnotit výsledky modelu proti testovací sadě dat:
In [33]:
Z_pred = np.around(model02.predict(Y_test, verbose=0))
metrics = pd.concat([metrics.drop(model02.name, level=0, errors='ignore'), model_quality_reporting(Z_test, Z_pred, model_name=model02.name)])
precision recall f1-score support
NORM 0.81 0.92 0.86 964
MI 0.81 0.62 0.70 553
STTC 0.78 0.71 0.74 523
CD 0.80 0.65 0.72 498
HYP 0.72 0.47 0.57 263
micro avg 0.80 0.73 0.76 2801
macro avg 0.78 0.67 0.72 2801
weighted avg 0.79 0.73 0.75 2801
samples avg 0.77 0.74 0.74 2801
Z Výše uvedené zprávy je zřejmé, že v tomto případě jsou výsledky již výrazně lepší. Model pokulhává především u klasifikační třídy HYP, kde metrikarecall a tedy takéf1-score není nic moc. Přisuzuji to především malému zastoupení vzorků s touto klasifikační třídou v celé datové sadě (viz mé poznámky při přípravě dat).
S model – pro spektrogramy křivek
2D konvoluce potřebuje datové sady rozšířené o jednu dimenzi, proto:
In [34]:
S_train = np.expand_dims(S_train, -1) S_valid = np.expand_dims(S_valid, -1) S_test = np.expand_dims(S_test, -1) print(f"S_train={S_train.shape} S_valid={S_valid.shape} S_test={S_test.shape}") S_train=(17441, 12, 31, 34, 1) S_valid=(2193, 12, 31, 34, 1) S_test=(2203, 12, 31, 34, 1)
Opět přichází na scénu na funkce, která vytvoří konvoluční vrstvy pro přepracování spektrogramů na features.
Na tomto místě musím zmínit ještě jednu věc, a sice to, že signál z každého svodu jsem přepočítal na samostatný spektrogram. Pokud z nich budu chtít vytvořit oddělené vlastnosti, pak to budu muset udělat v oddělených větvích. Proto jsem vytvořil samostatné 2D konvoluční vrstvy pro každý svod (ve funkci cyklím podle druhé dimenze):
In [35]:
def create_S_model(X, *, filters=(32, 64, 128), kernel_size=((3, 3), (3, 3), (3, 3)), strides=((1, 1), (1, 1), (1, 1))):
f1, f2, f3 = filters
k1, k2, k3 = kernel_size
s1, s2, s3 = strides
X = keras.layers.Normalization(axis=None, name='S_norm')(X)
lead_branches = []
for lead, x in enumerate(tf.split(X, X.shape[1], axis=1, name="S_split")):
x = tf.squeeze(x, axis=1, name=f'S_squeeze_{lead}')
x = keras.layers.Conv2D(f1, k1, strides=s1, padding='same', name=f'S_conv_{lead}_1')(x)
x = keras.layers.BatchNormalization(name=f'S_norm_{lead}_1')(x)
x = keras.layers.ReLU(name=f'S_relu_{lead}_1')(x)
x = keras.layers.MaxPool2D((2, 2), name=f'S_pool_{lead}_1')(x)
x = keras.layers.Conv2D(f2, k2, strides=s2, padding='same', name=f'S_conv_{lead}_2')(x)
x = keras.layers.BatchNormalization(name=f'S_norm_{lead}_2')(x)
x = keras.layers.ReLU(name=f'S_relu_{lead}_2')(x)
x = keras.layers.MaxPool2D((2, 2), name=f'S_pool_{lead}_2')(x)
x = keras.layers.Conv2D(f3, k3, strides=s3, padding='same', name=f'S_conv_{lead}_3')(x)
x = keras.layers.BatchNormalization(name=f'S_norm_{lead}_3')(x)
x = keras.layers.ReLU(name=f'S_relu_{lead}_3')(x)
x = keras.layers.MaxPool2D((2, 2), name=f'S_pool_{lead}_3')(x)
x = keras.layers.GlobalAveragePooling2D(name=f'S_aver_{lead}')(x)
x = tf.expand_dims(x, 1, name=f'S_expand_{lead}')
lead_branches.append(x)
X = keras.layers.Concatenate(axis=1, name="S_concat")(lead_branches)
X = keras.layers.Flatten(name="S_flatten")(X)
return X
Vytvářím tři bloky konvolučních vrstev, v tomto případě ale odděleně pro každý svod. Parametrem funkce je počet vlastností v každé vrstvě, velikost kernelu a krok konvoluce. Naleznete zde také vrstvy pro redukcí dimenzí, v tomto případě jak ve frekvenční tak v časové rovině. No a na závěr zpracování každé větve pak úplné potlačení těchto dimenzí s využitímGlobalAveragePooling2D vrstvy. Výsledek všech větví je pak vrstvouConcatenate spojen do jedné dimenze vlastností. Celý model je uveden vrstvou Normalization , která provede normalizaci všech spektrogramů podle jednoho společného průměru a směrodatné odchylky.
Doporučuji prohlédnou si výpis po překladu modelu. Transformace dimenzí tam bude asi přehlednější.
In [36]:
def create_model03(S_shape, Z_shape):
S_inputs = keras.Input(S_shape[1:], name='S_inputs')
X = create_S_model(S_inputs, filters=(32, 64, 128), kernel_size=((3, 3), (3, 3), (3, 3)))
X = keras.layers.Dense(128, activation='relu', name='Z_dense_1')(X)
X = keras.layers.Dense(128, activation='relu', name='Z_dense_2')(X)
X = keras.layers.Dropout(0.5, name='Z_drop_1')(X)
outputs = keras.layers.Dense(Z_shape[-1], activation='sigmoid', name='Z_outputs')(X)
model = keras.Model(inputs=S_inputs, outputs=outputs, name='S_model')
return model
Zvolil jsem narůstající počet vlastností postupně 32, 62 a 128. Kernely ve všech vrstvách jsou velikosti 3×3 hodnoty.
A nyní již může následovat překlad:
In [37]:
model03 = create_model03(S_train.shape, Z_train.shape) model03.compile(optimizer='adam', loss='binary_crossentropy', metrics=['binary_accuracy', 'Precision', 'Recall']) model03.summary() Model: "S_model" __________________________________________________________________________________________________ Layer (type) Output Shape Param # Connected to ================================================================================================== S_inputs (InputLayer) [(None, 12, 31, 34, 1)] 0 [] S_norm (Normalization) (None, 12, 31, 34, 1) 3 ['S_inputs[0][0]'] tf.split (TFOpLambda) [(None, 1, 31, 34, 1), 0 ['S_norm[0][0]'] (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1), (None, 1, 31, 34, 1)] tf.compat.v1.squeeze (TFOp (None, 31, 34, 1) 0 ['tf.split[0][0]'] Lambda) tf.compat.v1.squeeze_1 (TF (None, 31, 34, 1) 0 ['tf.split[0][1]'] OpLambda) tf.compat.v1.squeeze_2 (TF (None, 31, 34, 1) 0 ['tf.split[0][2]'] OpLambda) tf.compat.v1.squeeze_3 (TF (None, 31, 34, 1) 0 ['tf.split[0][3]'] OpLambda) tf.compat.v1.squeeze_4 (TF (None, 31, 34, 1) 0 ['tf.split[0][4]'] OpLambda) tf.compat.v1.squeeze_5 (TF (None, 31, 34, 1) 0 ['tf.split[0][5]'] OpLambda) tf.compat.v1.squeeze_6 (TF (None, 31, 34, 1) 0 ['tf.split[0][6]'] OpLambda) tf.compat.v1.squeeze_7 (TF (None, 31, 34, 1) 0 ['tf.split[0][7]'] OpLambda) tf.compat.v1.squeeze_8 (TF (None, 31, 34, 1) 0 ['tf.split[0][8]'] OpLambda) tf.compat.v1.squeeze_9 (TF (None, 31, 34, 1) 0 ['tf.split[0][9]'] OpLambda) tf.compat.v1.squeeze_10 (T (None, 31, 34, 1) 0 ['tf.split[0][10]'] FOpLambda) tf.compat.v1.squeeze_11 (T (None, 31, 34, 1) 0 ['tf.split[0][11]'] FOpLambda) S_conv_0_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze[0][0]'] S_conv_1_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_1[0][0] '] S_conv_2_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_2[0][0] '] S_conv_3_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_3[0][0] '] S_conv_4_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_4[0][0] '] S_conv_5_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_5[0][0] '] S_conv_6_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_6[0][0] '] S_conv_7_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_7[0][0] '] S_conv_8_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_8[0][0] '] S_conv_9_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_9[0][0] '] S_conv_10_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_10[0][0 ]'] S_conv_11_1 (Conv2D) (None, 31, 34, 32) 320 ['tf.compat.v1.squeeze_11[0][0 ]'] S_norm_0_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_0_1[0][0]'] tion) S_norm_1_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_1_1[0][0]'] tion) S_norm_2_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_2_1[0][0]'] tion) S_norm_3_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_3_1[0][0]'] tion) S_norm_4_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_4_1[0][0]'] tion) S_norm_5_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_5_1[0][0]'] tion) S_norm_6_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_6_1[0][0]'] tion) S_norm_7_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_7_1[0][0]'] tion) S_norm_8_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_8_1[0][0]'] tion) S_norm_9_1 (BatchNormaliza (None, 31, 34, 32) 128 ['S_conv_9_1[0][0]'] tion) S_norm_10_1 (BatchNormaliz (None, 31, 34, 32) 128 ['S_conv_10_1[0][0]'] ation) S_norm_11_1 (BatchNormaliz (None, 31, 34, 32) 128 ['S_conv_11_1[0][0]'] ation) S_relu_0_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_0_1[0][0]'] S_relu_1_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_1_1[0][0]'] S_relu_2_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_2_1[0][0]'] S_relu_3_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_3_1[0][0]'] S_relu_4_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_4_1[0][0]'] S_relu_5_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_5_1[0][0]'] S_relu_6_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_6_1[0][0]'] S_relu_7_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_7_1[0][0]'] S_relu_8_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_8_1[0][0]'] S_relu_9_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_9_1[0][0]'] S_relu_10_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_10_1[0][0]'] S_relu_11_1 (ReLU) (None, 31, 34, 32) 0 ['S_norm_11_1[0][0]'] S_pool_0_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_0_1[0][0]'] S_pool_1_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_1_1[0][0]'] S_pool_2_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_2_1[0][0]'] S_pool_3_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_3_1[0][0]'] S_pool_4_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_4_1[0][0]'] S_pool_5_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_5_1[0][0]'] S_pool_6_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_6_1[0][0]'] S_pool_7_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_7_1[0][0]'] S_pool_8_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_8_1[0][0]'] S_pool_9_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_9_1[0][0]'] S_pool_10_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_10_1[0][0]'] S_pool_11_1 (MaxPooling2D) (None, 15, 17, 32) 0 ['S_relu_11_1[0][0]'] S_conv_0_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_0_1[0][0]'] S_conv_1_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_1_1[0][0]'] S_conv_2_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_2_1[0][0]'] S_conv_3_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_3_1[0][0]'] S_conv_4_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_4_1[0][0]'] S_conv_5_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_5_1[0][0]'] S_conv_6_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_6_1[0][0]'] S_conv_7_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_7_1[0][0]'] S_conv_8_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_8_1[0][0]'] S_conv_9_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_9_1[0][0]'] S_conv_10_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_10_1[0][0]'] S_conv_11_2 (Conv2D) (None, 15, 17, 64) 18496 ['S_pool_11_1[0][0]'] S_norm_0_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_0_2[0][0]'] tion) S_norm_1_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_1_2[0][0]'] tion) S_norm_2_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_2_2[0][0]'] tion) S_norm_3_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_3_2[0][0]'] tion) S_norm_4_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_4_2[0][0]'] tion) S_norm_5_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_5_2[0][0]'] tion) S_norm_6_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_6_2[0][0]'] tion) S_norm_7_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_7_2[0][0]'] tion) S_norm_8_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_8_2[0][0]'] tion) S_norm_9_2 (BatchNormaliza (None, 15, 17, 64) 256 ['S_conv_9_2[0][0]'] tion) S_norm_10_2 (BatchNormaliz (None, 15, 17, 64) 256 ['S_conv_10_2[0][0]'] ation) S_norm_11_2 (BatchNormaliz (None, 15, 17, 64) 256 ['S_conv_11_2[0][0]'] ation) S_relu_0_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_0_2[0][0]'] S_relu_1_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_1_2[0][0]'] S_relu_2_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_2_2[0][0]'] S_relu_3_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_3_2[0][0]'] S_relu_4_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_4_2[0][0]'] S_relu_5_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_5_2[0][0]'] S_relu_6_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_6_2[0][0]'] S_relu_7_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_7_2[0][0]'] S_relu_8_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_8_2[0][0]'] S_relu_9_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_9_2[0][0]'] S_relu_10_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_10_2[0][0]'] S_relu_11_2 (ReLU) (None, 15, 17, 64) 0 ['S_norm_11_2[0][0]'] S_pool_0_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_0_2[0][0]'] S_pool_1_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_1_2[0][0]'] S_pool_2_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_2_2[0][0]'] S_pool_3_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_3_2[0][0]'] S_pool_4_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_4_2[0][0]'] S_pool_5_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_5_2[0][0]'] S_pool_6_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_6_2[0][0]'] S_pool_7_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_7_2[0][0]'] S_pool_8_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_8_2[0][0]'] S_pool_9_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_9_2[0][0]'] S_pool_10_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_10_2[0][0]'] S_pool_11_2 (MaxPooling2D) (None, 7, 8, 64) 0 ['S_relu_11_2[0][0]'] S_conv_0_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_0_2[0][0]'] S_conv_1_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_1_2[0][0]'] S_conv_2_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_2_2[0][0]'] S_conv_3_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_3_2[0][0]'] S_conv_4_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_4_2[0][0]'] S_conv_5_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_5_2[0][0]'] S_conv_6_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_6_2[0][0]'] S_conv_7_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_7_2[0][0]'] S_conv_8_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_8_2[0][0]'] S_conv_9_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_9_2[0][0]'] S_conv_10_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_10_2[0][0]'] S_conv_11_3 (Conv2D) (None, 7, 8, 128) 73856 ['S_pool_11_2[0][0]'] S_norm_0_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_0_3[0][0]'] tion) S_norm_1_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_1_3[0][0]'] tion) S_norm_2_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_2_3[0][0]'] tion) S_norm_3_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_3_3[0][0]'] tion) S_norm_4_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_4_3[0][0]'] tion) S_norm_5_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_5_3[0][0]'] tion) S_norm_6_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_6_3[0][0]'] tion) S_norm_7_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_7_3[0][0]'] tion) S_norm_8_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_8_3[0][0]'] tion) S_norm_9_3 (BatchNormaliza (None, 7, 8, 128) 512 ['S_conv_9_3[0][0]'] tion) S_norm_10_3 (BatchNormaliz (None, 7, 8, 128) 512 ['S_conv_10_3[0][0]'] ation) S_norm_11_3 (BatchNormaliz (None, 7, 8, 128) 512 ['S_conv_11_3[0][0]'] ation) S_relu_0_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_0_3[0][0]'] S_relu_1_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_1_3[0][0]'] S_relu_2_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_2_3[0][0]'] S_relu_3_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_3_3[0][0]'] S_relu_4_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_4_3[0][0]'] S_relu_5_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_5_3[0][0]'] S_relu_6_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_6_3[0][0]'] S_relu_7_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_7_3[0][0]'] S_relu_8_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_8_3[0][0]'] S_relu_9_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_9_3[0][0]'] S_relu_10_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_10_3[0][0]'] S_relu_11_3 (ReLU) (None, 7, 8, 128) 0 ['S_norm_11_3[0][0]'] S_pool_0_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_0_3[0][0]'] S_pool_1_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_1_3[0][0]'] S_pool_2_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_2_3[0][0]'] S_pool_3_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_3_3[0][0]'] S_pool_4_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_4_3[0][0]'] S_pool_5_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_5_3[0][0]'] S_pool_6_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_6_3[0][0]'] S_pool_7_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_7_3[0][0]'] S_pool_8_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_8_3[0][0]'] S_pool_9_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_9_3[0][0]'] S_pool_10_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_10_3[0][0]'] S_pool_11_3 (MaxPooling2D) (None, 3, 4, 128) 0 ['S_relu_11_3[0][0]'] S_aver_0 (GlobalAveragePoo (None, 128) 0 ['S_pool_0_3[0][0]'] ling2D) S_aver_1 (GlobalAveragePoo (None, 128) 0 ['S_pool_1_3[0][0]'] ling2D) S_aver_2 (GlobalAveragePoo (None, 128) 0 ['S_pool_2_3[0][0]'] ling2D) S_aver_3 (GlobalAveragePoo (None, 128) 0 ['S_pool_3_3[0][0]'] ling2D) S_aver_4 (GlobalAveragePoo (None, 128) 0 ['S_pool_4_3[0][0]'] ling2D) S_aver_5 (GlobalAveragePoo (None, 128) 0 ['S_pool_5_3[0][0]'] ling2D) S_aver_6 (GlobalAveragePoo (None, 128) 0 ['S_pool_6_3[0][0]'] ling2D) S_aver_7 (GlobalAveragePoo (None, 128) 0 ['S_pool_7_3[0][0]'] ling2D) S_aver_8 (GlobalAveragePoo (None, 128) 0 ['S_pool_8_3[0][0]'] ling2D) S_aver_9 (GlobalAveragePoo (None, 128) 0 ['S_pool_9_3[0][0]'] ling2D) S_aver_10 (GlobalAveragePo (None, 128) 0 ['S_pool_10_3[0][0]'] oling2D) S_aver_11 (GlobalAveragePo (None, 128) 0 ['S_pool_11_3[0][0]'] oling2D) tf.expand_dims (TFOpLambda (None, 1, 128) 0 ['S_aver_0[0][0]'] ) tf.expand_dims_1 (TFOpLamb (None, 1, 128) 0 ['S_aver_1[0][0]'] da) tf.expand_dims_2 (TFOpLamb (None, 1, 128) 0 ['S_aver_2[0][0]'] da) tf.expand_dims_3 (TFOpLamb (None, 1, 128) 0 ['S_aver_3[0][0]'] da) tf.expand_dims_4 (TFOpLamb (None, 1, 128) 0 ['S_aver_4[0][0]'] da) tf.expand_dims_5 (TFOpLamb (None, 1, 128) 0 ['S_aver_5[0][0]'] da) tf.expand_dims_6 (TFOpLamb (None, 1, 128) 0 ['S_aver_6[0][0]'] da) tf.expand_dims_7 (TFOpLamb (None, 1, 128) 0 ['S_aver_7[0][0]'] da) tf.expand_dims_8 (TFOpLamb (None, 1, 128) 0 ['S_aver_8[0][0]'] da) tf.expand_dims_9 (TFOpLamb (None, 1, 128) 0 ['S_aver_9[0][0]'] da) tf.expand_dims_10 (TFOpLam (None, 1, 128) 0 ['S_aver_10[0][0]'] bda) tf.expand_dims_11 (TFOpLam (None, 1, 128) 0 ['S_aver_11[0][0]'] bda) S_concat (Concatenate) (None, 12, 128) 0 ['tf.expand_dims[0][0]', 'tf.expand_dims_1[0][0]', 'tf.expand_dims_2[0][0]', 'tf.expand_dims_3[0][0]', 'tf.expand_dims_4[0][0]', 'tf.expand_dims_5[0][0]', 'tf.expand_dims_6[0][0]', 'tf.expand_dims_7[0][0]', 'tf.expand_dims_8[0][0]', 'tf.expand_dims_9[0][0]', 'tf.expand_dims_10[0][0]', 'tf.expand_dims_11[0][0]'] S_flatten (Flatten) (None, 1536) 0 ['S_concat[0][0]'] Z_dense_1 (Dense) (None, 128) 196736 ['S_flatten[0][0]'] Z_dense_2 (Dense) (None, 128) 16512 ['Z_dense_1[0][0]'] Z_drop_1 (Dropout) (None, 128) 0 ['Z_dense_2[0][0]'] Z_outputs (Dense) (None, 5) 645 ['Z_drop_1[0][0]'] ================================================================================================== Total params: 1336712 (5.10 MB) Trainable params: 1331333 (5.08 MB) Non-trainable params: 5379 (21.02 KB) __________________________________________________________________________________________________
Následuje trénování modelu:
In [38]:
MODEL_CHECKPOINT = '/kaggle/working/model/model03.ckpt' callbacks_list = [ keras.callbacks.EarlyStopping(monitor='val_binary_accuracy', patience=10), keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_binary_accuracy', save_best_only=True) ] history = model03.fit(S_train, Z_train, epochs=100, batch_size=32, callbacks=callbacks_list, validation_data=(S_valid, Z_valid)) model03 = keras.models.load_model(MODEL_CHECKPOINT) model03.save('/kaggle/working/model/model03.keras') Epoch 1/100 546/546 [==============================] - 62s 66ms/step - loss: 0.4174 - binary_accuracy: 0.8142 - precision: 0.6817 - recall: 0.5084 - val_loss: 0.3741 - val_binary_accuracy: 0.8337 - val_precision: 0.7169 - val_recall: 0.5772 Epoch 2/100 546/546 [==============================] - 35s 63ms/step - loss: 0.3655 - binary_accuracy: 0.8436 - precision: 0.7355 - recall: 0.6030 - val_loss: 0.3575 - val_binary_accuracy: 0.8409 - val_precision: 0.7449 - val_recall: 0.5740 Epoch 3/100 546/546 [==============================] - 16s 30ms/step - loss: 0.3469 - binary_accuracy: 0.8526 - precision: 0.7523 - recall: 0.6286 - val_loss: 0.3786 - val_binary_accuracy: 0.8320 - val_precision: 0.7163 - val_recall: 0.5676 Epoch 4/100 546/546 [==============================] - 34s 63ms/step - loss: 0.3342 - binary_accuracy: 0.8575 - precision: 0.7612 - recall: 0.6424 - val_loss: 0.3459 - val_binary_accuracy: 0.8522 - val_precision: 0.7225 - val_recall: 0.6846 Epoch 5/100 546/546 [==============================] - 16s 30ms/step - loss: 0.3315 - binary_accuracy: 0.8591 - precision: 0.7598 - recall: 0.6539 - val_loss: 0.3540 - val_binary_accuracy: 0.8516 - val_precision: 0.7537 - val_recall: 0.6233 Epoch 6/100 546/546 [==============================] - 16s 30ms/step - loss: 0.3186 - binary_accuracy: 0.8659 - precision: 0.7724 - recall: 0.6716 - val_loss: 0.3518 - val_binary_accuracy: 0.8468 - val_precision: 0.7528 - val_recall: 0.5965 Epoch 7/100 546/546 [==============================] - 34s 63ms/step - loss: 0.3097 - binary_accuracy: 0.8691 - precision: 0.7794 - recall: 0.6781 - val_loss: 0.3599 - val_binary_accuracy: 0.8532 - val_precision: 0.7529 - val_recall: 0.6336 Epoch 8/100 546/546 [==============================] - 34s 63ms/step - loss: 0.3048 - binary_accuracy: 0.8712 - precision: 0.7829 - recall: 0.6845 - val_loss: 0.3285 - val_binary_accuracy: 0.8589 - val_precision: 0.7526 - val_recall: 0.6675 Epoch 9/100 546/546 [==============================] - 16s 30ms/step - loss: 0.2985 - binary_accuracy: 0.8754 - precision: 0.7915 - recall: 0.6935 - val_loss: 0.3583 - val_binary_accuracy: 0.8420 - val_precision: 0.7284 - val_recall: 0.6086 Epoch 10/100 546/546 [==============================] - 17s 30ms/step - loss: 0.2919 - binary_accuracy: 0.8780 - precision: 0.7965 - recall: 0.7002 - val_loss: 0.4031 - val_binary_accuracy: 0.8202 - val_precision: 0.6635 - val_recall: 0.6022 Epoch 11/100 546/546 [==============================] - 34s 63ms/step - loss: 0.2826 - binary_accuracy: 0.8817 - precision: 0.8026 - recall: 0.7104 - val_loss: 0.3278 - val_binary_accuracy: 0.8605 - val_precision: 0.7835 - val_recall: 0.6275 Epoch 12/100 546/546 [==============================] - 35s 64ms/step - loss: 0.2760 - binary_accuracy: 0.8852 - precision: 0.8100 - recall: 0.7180 - val_loss: 0.3267 - val_binary_accuracy: 0.8613 - val_precision: 0.7483 - val_recall: 0.6893 Epoch 13/100 546/546 [==============================] - 34s 63ms/step - loss: 0.2705 - binary_accuracy: 0.8882 - precision: 0.8149 - recall: 0.7263 - val_loss: 0.3371 - val_binary_accuracy: 0.8621 - val_precision: 0.7534 - val_recall: 0.6846 Epoch 14/100 546/546 [==============================] - 17s 31ms/step - loss: 0.2627 - binary_accuracy: 0.8910 - precision: 0.8193 - recall: 0.7341 - val_loss: 0.4129 - val_binary_accuracy: 0.8244 - val_precision: 0.6660 - val_recall: 0.6283 Epoch 15/100 546/546 [==============================] - 16s 30ms/step - loss: 0.2544 - binary_accuracy: 0.8953 - precision: 0.8261 - recall: 0.7462 - val_loss: 0.3595 - val_binary_accuracy: 0.8416 - val_precision: 0.6992 - val_recall: 0.6675 Epoch 16/100 546/546 [==============================] - 17s 30ms/step - loss: 0.2460 - binary_accuracy: 0.8988 - precision: 0.8361 - recall: 0.7501 - val_loss: 0.3900 - val_binary_accuracy: 0.8522 - val_precision: 0.7667 - val_recall: 0.6061 Epoch 17/100 546/546 [==============================] - 17s 30ms/step - loss: 0.2364 - binary_accuracy: 0.9046 - precision: 0.8438 - recall: 0.7678 - val_loss: 0.3842 - val_binary_accuracy: 0.8421 - val_precision: 0.6780 - val_recall: 0.7285 Epoch 18/100 546/546 [==============================] - 17s 30ms/step - loss: 0.2307 - binary_accuracy: 0.9062 - precision: 0.8462 - recall: 0.7724 - val_loss: 0.3902 - val_binary_accuracy: 0.8523 - val_precision: 0.7487 - val_recall: 0.6357 Epoch 19/100 546/546 [==============================] - 16s 30ms/step - loss: 0.2180 - binary_accuracy: 0.9126 - precision: 0.8597 - recall: 0.7850 - val_loss: 0.4497 - val_binary_accuracy: 0.8565 - val_precision: 0.7513 - val_recall: 0.6554 Epoch 20/100 546/546 [==============================] - 16s 30ms/step - loss: 0.2098 - binary_accuracy: 0.9157 - precision: 0.8629 - recall: 0.7954 - val_loss: 0.4039 - val_binary_accuracy: 0.8544 - val_precision: 0.7434 - val_recall: 0.6575 Epoch 21/100 546/546 [==============================] - 16s 30ms/step - loss: 0.1974 - binary_accuracy: 0.9212 - precision: 0.8743 - recall: 0.8067 - val_loss: 0.5562 - val_binary_accuracy: 0.8031 - val_precision: 0.6326 - val_recall: 0.5480 Epoch 22/100 546/546 [==============================] - 17s 30ms/step - loss: 0.1954 - binary_accuracy: 0.9210 - precision: 0.8732 - recall: 0.8072 - val_loss: 0.5557 - val_binary_accuracy: 0.7650 - val_precision: 0.5376 - val_recall: 0.5762 Epoch 23/100 546/546 [==============================] - 16s 30ms/step - loss: 0.1851 - binary_accuracy: 0.9265 - precision: 0.8832 - recall: 0.8201 - val_loss: 0.5077 - val_binary_accuracy: 0.8196 - val_precision: 0.6461 - val_recall: 0.6507
A takto vypadal průběh trénování z pohledu optimalizované funkce a metrik:
In [39]:
sns.relplot(data=pd.DataFrame(history.history), kind='line', height=4, aspect=4)
plt.show()
A nyní si můžu model opět vyhodnotit proti testovací sadě dat:
In [40]:
Z_pred = np.around(model03.predict(S_test, verbose=0))
metrics = pd.concat([metrics.drop(model03.name, level=0, errors='ignore'), model_quality_reporting(Z_test, Z_pred, model_name=model03.name)])
precision recall f1-score support
NORM 0.80 0.85 0.82 964
MI 0.65 0.62 0.64 553
STTC 0.81 0.54 0.64 523
CD 0.74 0.64 0.69 498
HYP 0.57 0.58 0.57 263
micro avg 0.74 0.68 0.71 2801
macro avg 0.71 0.65 0.67 2801
weighted avg 0.74 0.68 0.71 2801
samples avg 0.70 0.69 0.68 2801
Výsledky nejsou výrazně lepší, než tomu bylo u předchozího modelu, ale jsou poněkud rovnoměrnější pro všechny klasifikační třídy.
V příštím dílu budu pokračovat kombinovanými modely.
Přidat názor
