Mravenčí kolonií na Nurikabe

Algoritmus mravenčí kolonie (Ant colony optimization algorithms, ACO) patří do rodiny pravděpodobnostních optimalizačních algoritmů zaměřených na hledání cest v grafech. Je pokusem napodobit chování mravenčí kolonie při hledání co nejkratší cesty k potravě.

Více informací o algoritmu můžete najít například: Ant colony optimization algorithms

Jak takový algoritmus funguje si člověk nejlépe vyzkouší při řešení nějakého konkrétního problému. Vybral jsem si hru Nurikabe.

Nurikabe je logická desková hra ze skupiny publikované Nikoli. Cílem je vyznačit na desce ostrovy o požadované velikosti, a to tak, aby se ostrovy vzájemně nedotýkaly a voda mezi ostrovy byla spojitá.

Základní pravidla lze shrnout do několika bodů:

• zadáním hry je deska rozdělená na čtvercová pole; některá z polí nesou číselnou hodnotu, která představuje velikost ostrova v daním místě

• vyznačené ostrovy se nesmí dotýkat svými okraji (dotyk rohem je povolen)

• voda mezi ostrovy musí být jedna spojitá oblast

• voda nesmí obsahovat „tůně“, tedy čtverce 2×2, kde jsou všechny dlaždice označeny za vodu

Více informací o hře najdete například zde: Nurikabe (pozzle).

Pokud byste si chtěli zkusit vyřešit nějakou hru, pak můžete např. Nurikabe – online logická hra.

Při svém experimentu jsem vycházel především z následující práce: Solving Nurikabe with Ant Colony Optimization (Extended version)

Nurikabe se hraje na obdélníkové nebo čtvercové desce rozdělené na samostatné pole. Proto jsem pro implementaci algoritmu hojně využíval knihovnu Numpy a operace se dvourozměrnými poli.

V tomto textu uvádím pouze významné části algoritmu, které si zasluhují komentář. Pro ty z vás, kteří byste chtěli zkusit experimentovat s ACO, je k dispozici kompletní zdrojový kód nurikabe.ipynb.

Zevrubný popis AOC

Jak jsem již uvedl dříve, AOC je primárně zaměřen na hledání optimálních cest v grafech. V mám případě je takovým grafem deska hry rozdělená na dlaždice. Do grafu je postupně vypuštěno několik mravenců, kteří náhodně hledají nějaké řešení. V případě, že je řešení mravencem nalezeno, je jeho úspěšnost ohodnocena. Podle úspěšnosti řešení je pak na desce zanechána „feromonová stopa“, která slouží jako vodítko pro následující mravence.

Podstatou algoritmu je tedy jistá forma komunikace mezi mravenci na základě síly feromonové stopy zanechané předchůdci.

BoardSolution – jeden mravenec na desce

Tato třída implementuje řešení desky pro jednoho mravence.

Cílem je navrhnout rozložení ostrovů na desce co nejlépe tak, aby vyhovovaly zadání. Ono se to nemusí podařit úplně správně, proto je každé řešení možné ohodnotit celým číslem vyjadřující, jak dobře vyhovuje zadání.

Nejdříve ukážu odpovídající část kódu, a pak bude následovat vysvětlení pro podstatné části:

class BoardSolution:

    def __init__(self, shape, clues, pheromone_matrix):
        self.clues = clues
        self.pheromone_matrix = pheromone_matrix
        self.tiles_to_allocate = sum(clues.values())
        self.board = np.full(shape, BLACK, dtype=int)
        for coord in clues.keys():
            self.board[coord] = clues[coord]

    def score(self):
        missing_tiles = self.tiles_to_allocate - int((np.array(self.board >= 0, dtype=np.uint8).sum()))
        squares = sum((int(np.sum(self.board[r:r + 2, c:c + 2] == BLACK) == 4) for r in range(self.board.shape[0] - 1) for c in range(self.board.shape[1] - 1)))
        return missing_tiles + squares

    def expand_island(self, coord):
        region = {coord}

        def is_fragmented():
            water = np.array(self.board == -1, dtype=np.uint8)

            def fill_region(coord):
                if water[coord] == 1:
                    water[coord] = 0
                    for c in neighbours(coord, water.shape):
                        fill_region(c)

            r, c = np.argwhere(water == 1)[0]
            fill_region((int(r), int(c)))
            return np.sum(water) > 0

        def fragments_board(coord):
            self.board[coord] = WHITE
            result = is_fragmented()
            self.board[coord] = BLACK
            return result

        def choose_one(coordinates):
            value, pick = 0.0, random.uniform(0, sum(self.pheromone_matrix[c] for c in coordinates))
            for c in coordinates:
                value += self.pheromone_matrix[c]
                if value >= pick:
                    return c

        def expand_region():
            if self.board[coord] > len(region):
                adjacent = {c for c in neighbours_for_region(region, self.board.shape) if self.board[c] == BLACK}
                allocated_to_others = {c for c in adjacent for n in neighbours(c, self.board.shape) if self.board[n] != BLACK and n not in region}
                acceptable = {c for c in adjacent.difference(allocated_to_others) if not fragments_board(c)}
                if acceptable:
                    c = choose_one(acceptable)
                    self.board[c] = WHITE
                    region.add(c)
                    expand_region()
        expand_region()

    def solve(self):
        all_islands = [(int(r), int(c)) for r, c in np.argwhere(self.board > 0)]
        random.shuffle(all_islands)
        for coord in all_islands:
            self.expand_island(coord)
        return self.score()

Do konstruktoru třídy se předávají tři parametry:

• shape – rozměry hrací desky

• clues – vodítka umístění ostrovů, tedy souřadnice a jejich velikosti

• pheromone_matrix – matice feromonové stopy zanechané předchozími řešeními (jedná se o kopii centrální matice, takže s ní můžu na úrovni této třídy manipulovat)

Dále si v konstruktoru vytvořím obraz desky, do které jsou zaneseny souřadnice a velikosti ostrovů, a zbytek je tvořen vodou.

metoda solve()

Hlavní výkonná metoda, která zajistí vytvoření jednoho řešení desky dle zadání.

Postupně procházím všechna vodítka pro ostrovy v náhodném pořadí. Pro každé vodítko se pokusím alokovat na desce ostrov požadované velikosti. Výsledkem metody je pak hodnocení úspěšnosti řešení.

metoda score()

Metoda mně vrátí číslo hodnotící, jak moc mé řešení vyhovuje zadání.

Jedná se o součet dvou hodnot. První je rozdíl mezi požadovanou velikostí všech ostrovů a skutečně alokovanou velikostí. Čím je číslo větší, tím méně úspěšný jsem při vytváření ostrovů byl. Druhým číslem je počet tůní, které v řešení zbyly.

Z výše uvedeného vyplývá, že ohodnocení kompletního a správného řešení desky je 0. Pokud je skóre větší jak nula, pak jsou v něm chyby.

metoda expand_island(coord)

Toto je ta zásadní část řešení pro jednoho mravence. Úkolem metody je alokovat ostrov na aktuální desce. Parametrem je souřadnice vodítka pro tento ostrov.

Souřadnice vodítka se stávají první dlaždicí zařazenou do ostrova. Následně rekurzivně opakuji funkci expand_region(), která se pokusí k ostrovu přidat další dlaždici, a to tak dlouho, dokud není ostrov požadované velikosti, nebo dokud již není možné žádnou dlaždici přidat (bez porušení pravidel hry).

A jak přidám další dlaždici k ostrovu? Postup je následující:

• vyhledám množinu všech dlaždic, které jsou sousední k existujícímu ostrovu

• z této množiny vyhodím ty, které sousedí s jinými ostrovy (kdybych takovou dlaždici použil, pak by se dva ostrovy začaly dotýkat)

• z výsledné množiny ještě vyhodím ty, které sice můžu alokovat, ale které mně způsobí fragmentaci vodní plochy. Jedná se o funkci fragments_board(coord), která dočasně označí dlaždici za alokovanou, a pak zkouší, jestli je voda stále spojitá (je zde použita rekurzivní podoba DFS)

• nyní mám tedy množinu dlaždic, z niž si musím jednu vybrat a zařadit jí k ostrovu. Ale kterou? Zde přichází ke slovu funkce choose_one(coordinates) a feromonová matice předaná do konstruktoru. Z té si zjistím sílu feromonu pro každou dlaždici. Z množiny vybírám náhodně jednu s pravděpodobností odpovídající síle feromonu (metoda obvykle označovaná jako “roulette wheel”).

• v případě, že jsem předchozími kroky vybral jednu dlaždici, zařadím ji do ostrova

AntColony – mnoho mravenců s jedním cílem

Nyní se dostávám k jádru algoritmu Ant Colony Optimization.

Podstatou algoritmu je postupná produkce generace mravenců, kteří každý vytváří své vlastní řešení problému (hledá cestu k jídlu). Z generace je následně vybrán jeden mravenec s nejlepším řešením (měřeno velikostí skóre), a toto řešení je zohledněno v aktualizaci globální feromonové stopy.

Tato globální feromonová stopa se stává vodítkem pro následující generaci mravenců, a to vše tak dlouho, dokud nenajdu vyhovující řešení, nebo nevyčerpám limit generací.

Takto vypadá třída, která postup implementuje:

class AntColony:

    ANTS_PER_GENERATION = 10
    GENERATIONS = 300

    LOCAL_PHEROMONE_UPDATE = 0.5
    GLOBAL_EVAPORATION = 0.2
    TAU_EVAPORATION = 0.1

    def __init__(self, shape, islands):
        self.shape = shape
        self.clues = islands
        self.tau0 = 1.0 / sum(islands.values())
        self.pheromone_matrix = np.full(shape, self.tau0, dtype=np.float16)
        self.pheromone_history = [np.copy(self.pheromone_matrix)]
        self.solution = None

    def generation(self, pheromone_matrix):
        best_score, best_solution = reduce(lambda x, y: x * y, self.shape), None
        for _ in range(AntColony.ANTS_PER_GENERATION):
            solution = BoardSolution(self.shape, self.clues, pheromone_matrix)
            score = solution.solve()
            if score == 0:
                return solution
            elif score < best_score:
                best_score, best_solution = score, solution
            verbose('.', end='')
            np.putmask(pheromone_matrix, solution.board >= WHITE, (1.0 - AntColony.LOCAL_PHEROMONE_UPDATE) * pheromone_matrix + AntColony.LOCAL_PHEROMONE_UPDATE * self.tau0)
        return best_solution

    def solve(self):
        tau_best = self.tau0
        for generation in range(AntColony.GENERATIONS):
            verbose(f"Generation: {generation}: ", end='')
            solution = self.generation(np.copy(self.pheromone_matrix))
            score = solution.score()
            if score == 0:
                self.solution = solution
                verbose(" solution found")
                return True
            verbose(f" best score: {score}, pheromone max: {self.pheromone_matrix.max():.4f}")
            tau = 1.0 / score
            if tau > tau_best:
                np.putmask(self.pheromone_matrix, solution.board >= WHITE, ((1.0 - AntColony.GLOBAL_EVAPORATION) * self.pheromone_matrix + AntColony.GLOBAL_EVAPORATION * tau).astype(np.float16))
                self.pheromone_history.append(np.copy(self.pheromone_matrix))
                tau_best = tau
            tau_best = (1.0 - AntColony.TAU_EVAPORATION) * tau_best
        return False

Do konstruktoru třídy se předávají dva parametry:

• shape – rozměry hrací desky

• islands – vodítka umístění ostrovů, tedy souřadnice a jejich velikosti

Dále se v rámci konstruktoru inicializuje globální feromonová stopa pheromone_matrix. Jedná se o pole ve stejném rozměru jako je hrací deska. Na počátku je hodnota feromonu pro každou dlaždici nastavena na hodnotu tau0.

metoda solve()

Jedná se o hlavní výkonnou metodu třídy. Opakovaně vytváří generace mravenců voláním metody generation(). Výsledkem je nejlepší řešení mravence z dané generace.

V případě, že získané řešení vyhovuje zadání, mám výsledek a končím.

V opačném případě:

• zjistím skóre řešení a jemu odpovídající přírůstek feromonu

• pokud je přírůstek feromonu lepší než aktuálně nejlepší, pak podle alokovaných dlaždic řešení aktualizuji globální feromonovou mapu. Při aktualizaci se používá jako parametr GLOBAL_EVAPORATION, který zajišťuje postupné „vyprchávání“ feromonu u dlaždic, které jsou méně alokované

• na konci cyklu je ještě zařazena postupná redukce hodnoty nejlepší feromonové stopy parametrem TAU_EVAPORATION. Autoři výše uvedené studie tento krok zařadili proto, aby bránili rychlé konvergenci k lokálnímu minimu, a tedy překážce k nalezení vyhovujícího řešení.

metoda generation(pheromone_matrix)

Implementuje nezbytné kroky pro provedení jedné generace mravenců a nalezení nejlepšího řešení.

Jako parametr dostává kopii globální feromonové mapy. A k čemu jí vlastně potřebuje? Otázka je, jakou generaci mravenců já vlastně preferuji. Pokud by všichni mravenci v generaci postupovali podle globální feromonové stopy, pak by vytvářeli velice podobná řešení. No a to asi úplně nechci. Mně by se hodilo, aby v rámci jedné generace mravenci vytvářeli co nejširší škálu možných řešení, abych si měl z čeho vybírat. A proto tady je lokální feromonová mapa.

V generaci se postupně vytváří mravenci (dáno parametrem ANTS_PER_GENERATION) a ti budují své vlastní řešení na základě lokální feromonové mapy. Když mravenec dokončí své řešení, pak feromon dlaždic alokovaný v rámci řešení je snížen oproti původní hodnotě (řízeno parametrem LOCAL_PHEROMONE_UPDATE). Takto aktualizovaná lokální feromonová mapa je podkladem pro řešení dalšího mravence v generaci. Pokud tedy předchůdce použil dlaždici ve svém řešení, pak se snižuje pravděpodobnost, že jí použije i jeho následovník. A to je celé.

Na konci svého běhu pak metoda vrátí řešení s nejnižším skóre.

Experiment

Jako první pokus jsem si vybral následující vzorek Nurikabe o velikosti 7×7 dlaždic:

SAMPLE = 2

source = SampleSource()
print(source[SAMPLE])
[[0 6 0 0 0 2 0]
 [0 0 0 0 0 0 0]
 [0 0 3 0 2 0 0]
 [0 0 0 0 0 0 0]
 [0 0 3 0 2 0 0]
 [0 0 0 0 0 0 0]
 [0 2 0 0 0 1 0]]

colony = AntColony(**source.sample(SAMPLE))
colony.solve()
Generation: 0: .......... best score: 3, pheromone max: 0.0476
Generation: 1: .......... best score: 3, pheromone max: 0.1047
Generation: 2: .......... best score: 3, pheromone max: 0.1504
Generation: 3: .......... best score: 3, pheromone max: 0.1870
Generation: 4: .......... best score: 3, pheromone max: 0.2162
Generation: 5: .. solution found

A takto vypadá řešení, které bylo AOC nalezeno:

image = (colony.solution.board >= WHITE).astype(np.float16)

fig=plt.figure(figsize=(3, 3))
plt.imshow(image, cmap='gray')
plt.show()

Následující vzorek je již poněkud větší, a sice 10×10 dlaždic:

SAMPLE = 5

source = SampleSource()
print(source[SAMPLE])
[[0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 2 0 0]
 [0 5 0 0 0 0 0 0 0 4]
 [0 0 9 0 0 0 0 0 2 0]
 [0 2 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0]
 [0 1 0 0 0 0 0 0 0 0]
 [2 0 8 0 0 0 0 0 0 0]
 [0 0 0 0 3 0 0 0 1 0]
 [0 0 1 0 0 0 0 0 0 0]]

colony = AntColony(**source.sample(SAMPLE))
colony.solve()
Generation: 0: .......... best score: 5, pheromone max: 0.0250
Generation: 1: .......... best score: 9, pheromone max: 0.0600
Generation: 2: .......... best score: 10, pheromone max: 0.0600
Generation: 3: .......... best score: 13, pheromone max: 0.0600
Generation: 4: .......... best score: 4, pheromone max: 0.0600
Generation: 5: .......... best score: 17, pheromone max: 0.0980
Generation: 6: .......... best score: 8, pheromone max: 0.0980
Generation: 7: .......... best score: 7, pheromone max: 0.0980
Generation: 8: .......... best score: 11, pheromone max: 0.0980
Generation: 9: .......... best score: 6, pheromone max: 0.0980
Generation: 10: .......... best score: 5, pheromone max: 0.1117
Generation: 11: .......... best score: 6, pheromone max: 0.1294
Generation: 12: .......... best score: 7, pheromone max: 0.1294
Generation: 13: .......... best score: 8, pheromone max: 0.1294
Generation: 14: .......... best score: 6, pheromone max: 0.1294
Generation: 15: .......... best score: 11, pheromone max: 0.1368
Generation: 16: .......... best score: 9, pheromone max: 0.1368
Generation: 17: .......... best score: 17, pheromone max: 0.1368
Generation: 18: .......... best score: 4, pheromone max: 0.1368
Generation: 19: .......... best score: 6, pheromone max: 0.1594
Generation: 20: .......... best score: 14, pheromone max: 0.1594
Generation: 21: .......... best score: 6, pheromone max: 0.1594
Generation: 22: .......... best score: 6, pheromone max: 0.1594
Generation: 23: .......... best score: 3, pheromone max: 0.1609
Generation: 24: .......... best score: 6, pheromone max: 0.1953
Generation: 25: .......... best score: 4, pheromone max: 0.1953
Generation: 26: .......... best score: 10, pheromone max: 0.1953
Generation: 27: .......... best score: 2, pheromone max: 0.1953
Generation: 28: .......... best score: 5, pheromone max: 0.2563
Generation: 29: .. solution found

Opět se můžete podívat na to, co bylo nalezeno jako řešení:

image = (colony.solution.board >= WHITE).astype(np.float16)

fig=plt.figure(figsize=(3, 3))
plt.imshow(image, cmap='gray')
plt.show()

Ještě vám ukážu, jak se postupně vyvíjela globální feromonová stopa:

cols = 6
rows = len(colony.pheromone_history) // cols + int(len(colony.pheromone_history) % cols)

image_max_value = max([h.max() for h in colony.pheromone_history])

fig=plt.figure(figsize=(20, 3 * rows))

for i, image in enumerate(colony.pheromone_history, start=1):
    fig.add_subplot(rows, cols, i)
    plt.imshow(image / image_max_value, cmap='gray', norm=matplotlib.colors.NoNorm())
plt.show()

A jako poslední ukázka mi poslouží zadání o velikosti 12×12 dlaždic:

SAMPLE = 6

source = SampleSource()
print(source[SAMPLE])
[[1 0 0 8 0 2 0 0 0 0 0 0]
 [0 5 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 5 0 0 0 0 2 0]
 [0 0 0 0 0 0 0 0 0 0 0 1]
 [0 0 0 0 0 0 0 0 0 0 0 0]
 [0 0 0 2 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 4 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 0 0]
 [3 0 0 0 0 0 0 0 0 0 0 0]
 [0 2 0 0 0 0 5 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 0 9 0]
 [0 0 0 0 0 0 5 0 5 0 0 1]]

colony = AntColony(**source.sample(SAMPLE))
colony.solve()
Generation: 0: .......... best score: 14, pheromone max: 0.0167
Generation: 1: .......... best score: 27, pheromone max: 0.0276
Generation: 2: .......... best score: 27, pheromone max: 0.0276
Generation: 3: .......... best score: 26, pheromone max: 0.0276
Generation: 4: .......... best score: 33, pheromone max: 0.0276
Generation: 5: .......... best score: 21, pheromone max: 0.0276
Generation: 6: .......... best score: 26, pheromone max: 0.0316
Generation: 7: .......... best score: 22, pheromone max: 0.0316
Generation: 8: .......... best score: 22, pheromone max: 0.0344
Generation: 9: .......... best score: 17, pheromone max: 0.0366
Generation: 10: .......... best score: 22, pheromone max: 0.0410
Generation: 11: .......... best score: 27, pheromone max: 0.0410
Generation: 12: .......... best score: 21, pheromone max: 0.0410
Generation: 13: .......... best score: 22, pheromone max: 0.0423
Generation: 14: .......... best score: 26, pheromone max: 0.0429
Generation: 15: .......... best score: 25, pheromone max: 0.0429
Generation: 16: .......... best score: 22, pheromone max: 0.0429
Generation: 17: .......... best score: 16, pheromone max: 0.0434
Generation: 18: .......... best score: 29, pheromone max: 0.0472
Generation: 19: .......... best score: 20, pheromone max: 0.0472
Generation: 20: .......... best score: 13, pheromone max: 0.0472
Generation: 21: .......... best score: 24, pheromone max: 0.0532
Generation: 22: .......... best score: 26, pheromone max: 0.0532
Generation: 23: .......... best score: 18, pheromone max: 0.0532
Generation: 24: .......... best score: 29, pheromone max: 0.0532
Generation: 25: .......... best score: 22, pheromone max: 0.0532
Generation: 26: .......... best score: 29, pheromone max: 0.0528
Generation: 27: .......... best score: 19, pheromone max: 0.0528
Generation: 28: .......... best score: 29, pheromone max: 0.0528
Generation: 29: .......... best score: 21, pheromone max: 0.0528
Generation: 30: .......... best score: 27, pheromone max: 0.0518
Generation: 31: .......... best score: 28, pheromone max: 0.0518
Generation: 32: .......... best score: 16, pheromone max: 0.0518
Generation: 33: .......... best score: 22, pheromone max: 0.0539
Generation: 34: .......... best score: 22, pheromone max: 0.0539
Generation: 35: .......... best score: 17, pheromone max: 0.0539
Generation: 36: .......... best score: 21, pheromone max: 0.0549
Generation: 37: .......... best score: 26, pheromone max: 0.0549
Generation: 38: .......... best score: 32, pheromone max: 0.0549
Generation: 39: .......... best score: 19, pheromone max: 0.0549
Generation: 40: .......... best score: 22, pheromone max: 0.0544
Generation: 41: .......... best score: 26, pheromone max: 0.0544
Generation: 42: .......... best score: 32, pheromone max: 0.0544
Generation: 43: .......... best score: 25, pheromone max: 0.0544
Generation: 44: .......... best score: 12, pheromone max: 0.0539
Generation: 45: .......... best score: 22, pheromone max: 0.0598
Generation: 46: .......... best score: 24, pheromone max: 0.0598
Generation: 47: .......... best score: 21, pheromone max: 0.0598
Generation: 48: .......... best score: 15, pheromone max: 0.0598
Generation: 49: .......... best score: 27, pheromone max: 0.0612
Generation: 50: .......... best score: 15, pheromone max: 0.0612
Generation: 51: . solution found

Takto vypadá nalezený výsledek včetně zobrazení globální feromonové stopy:

image = (colony.solution.board >= WHITE).astype(np.float16)

fig=plt.figure(figsize=(3, 3))
plt.imshow(image, cmap='gray')
plt.show()

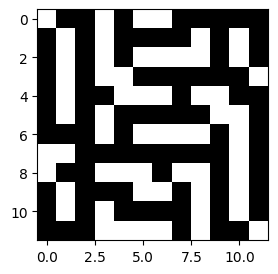
cols = 6
rows = len(colony.pheromone_history) // cols + int(len(colony.pheromone_history) % cols)

image_max_value = max([h.max() for h in colony.pheromone_history])

fig=plt.figure(figsize=(20, 3 * rows))

for i, image in enumerate(colony.pheromone_history, start=1):
    fig.add_subplot(rows, cols, i)
    plt.imshow(image / image_max_value, cmap='gray', norm=matplotlib.colors.NoNorm())
plt.show()

Závěrečné poznámky

To, že jsem vám tady ukázal příklady které vyšly neznamená, že tomu tak je vždy. AOC je pravděpodobnostní algoritmus, který má pomáhat při nalezení „dostatečně dobrého řešení“. V případě logické hry je řešení buď dobré nebo špatné a nic mezi tím. U větších zadání mně ani těch 300 generací nestačilo pro nalezení správného řešení.

Autoři výše uvedené studie ještě experimentovali v několika oblastech:

• pořadí výběru ostrovů, které mravenec v rámci svého řešení navštíví. Zkoušeli řazení dle velikosti, jejich vzájemné polohy a pod. Já jsem použil pouze náhodný výběr.

• výběr dlaždice z možných pro rozšíření ostrova, algoritmus „roulette wheel“ kombinovali výběrem s nejvyšší hodnotou