Lokalizace infekce malárie - klasifikační model a heatmap

6. 9. 2024 0:00 Jiří Raška

Tímto příspěvkem bych chtěl volně navázat na předchozí články zabývající se klasifikací obrázků do několika tříd. V těch dřívějších článcích se jednalo o rozpoznání zápalu plic na základě RTG snímků.

Pokud bych měl rychle shrnout jejich obsah, pak se jednalo o to, že jsem měl k dispozici snímky zdravých plic a snímky se zápalem. Úkolem hledaných modelů bylo najím způsob, jak rozlišit jedny od druhých. Jedná se tedy o běžně studovanou metodu klasifikace snímků na základě dříve připravených vzorků dat (tzv. supervised machine learning).

Otázka je, zda by se z této metody nedalo vytěžit více. Co kdyby mne zajímalo nejen to, že na vybraném snímku je nějaký problém, ale také místo snímku, kde ten problém je. Dalo by se inkriminované místo na snímku najít, aniž bych jej dříve měl označené na trénovacích datech?

Na tyto otázky se pokusím odpovědět v následujících odstavcích článku.

Nejdříve pouze základní příprava prostředí:

import sys
import os
import shutil
import warnings
import glob

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from tqdm import tqdm

import tensorflow as tf
import tensorflow.keras as keras

from keras import Input, Model
from keras import layers

from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix

from skimage.feature import peak_local_max

from matplotlib.patches import Rectangle

import cv2

sns.set_style('darkgrid')

warnings.simplefilter(action='ignore', category=FutureWarning)

import random

def seed_all(value=42):
    random.seed(value)
    np.random.seed(value)
    tf.random.set_seed(value)
    os.environ['PYTHONHASHSEED'] = str(value)

seed_all()

Datová sada

Pro své pokusy jsem si vybral datovou sadu Malaria Cell Images Dataset. V této datové sadě se dají najít dvě skupiny snímků buněk. První skupina snímků jsou ty, které jsou infikovány malárií. Druhá skupina jsou pak snímky buněk zdravých. Mám tedy k dispozici dvě třídy pro klasifikaci.

Vzhledem k počtu snímků budu všechny načítat jako RGB v menším rozlišení 64×64 bodů.

IMAGE_ROOT  = "/kaggle/input/cell-images-for-detecting-malaria/cell_images"

LABELS = ['Uninfected', 'Parasitized']

IMAGE_SIZE = (64, 64)

def get_data():
    x, y = list(), list()

    for i, label in enumerate(LABELS):
        for fn in tqdm(glob.glob(os.path.join(IMAGE_ROOT, label, '*.png')), desc=label):
            image = cv2.imread(fn, flags=cv2.IMREAD_COLOR)
            image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
            image = cv2.resize(image, IMAGE_SIZE).astype(np.float32) / 255.0
            x.append(image)
            y.append(i)

    perm = np.random.permutation(len(x))

    return np.array(x)[perm], np.eye(2)[y].astype(np.float32)[perm]

x, y = get_data()
Uninfected: 100%|██████████| 13779/13779 [01:24<00:00, 162.23it/s]
Parasitized: 100%|██████████| 13779/13779 [01:28<00:00, 155.96it/s]

Takto vypadají neinfikované vzorky:

samples = x[y[:, 0].astype(np.bool_)]

rows, cols = 2, 5
fig=plt.figure(figsize=(14, 6))
for i in range(1, rows*cols+1):
    fig.add_subplot(rows, cols, i)
    image = samples[random.randrange(samples.shape[0])]
    plt.imshow(image)
plt.show()

A takto vypadají vzorky infikované malárií:

samples = x[y[:, 1].astype(np.bool_)]

rows, cols = 2, 5
fig=plt.figure(figsize=(14, 6))
for i in range(1, rows*cols+1):
    fig.add_subplot(rows, cols, i)
    image = samples[random.randrange(samples.shape[0])]
    plt.imshow(image)
plt.show()

Jako obvykle si ještě všechna data rozdělím na dvě skupiny, první pro trénování a druhá pro ověření výsledků modelu:

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
(22046, 64, 64, 3) (22046, 2)
(5512, 64, 64, 3) (5512, 2)

Klasifikační model

Klasifikační model bude víceméně klasický, postavený na konvolučních vrstvách tak, jak je obvyklé ve VGG16 modelech.

Pro zlepšení výsledků učení jsem do modelu doplnil také vrstvy pro úpravu obrázků:

data_augmentation = keras.Sequential([
        layers.Normalization(),
        layers.RandomFlip("horizontal"),
        layers.RandomRotation(factor=0.2),
        layers.RandomZoom(height_factor=0.2, width_factor=0.2),    
], name="data_augmentation")

data_augmentation.layers[0].adapt(x_train)

Takto vypadá funkce, která mi vytvoří model v základní podobě:

def create_model(X_shape, classes=2, name="Model"):

    def conv_block(x, filters, *, kernels=None, steps=None, pooling=True, name=""):
        for i in range(len(filters)):
            x = layers.Conv2D(filters[i], kernels[i] if kernels else (3, 3), strides=steps[i] if steps else (1, 1), padding='same', name=f'{name}_conv_{i}')(x)
            x = layers.BatchNormalization(name=f'{name}_norm_{i}')(x)
            x = layers.Activation('relu', name=f'{name}_relu_{i}')(x)
        if pooling:
            x = layers.MaxPooling2D((2, 2), name=f'{name}_maxpool')(x)
        return x

    inputs = x = Input(X_shape[-3:], name='inputs')

    x = data_augmentation(inputs)

    x = conv_block(x, (64, 64), name="block_1")
    x = conv_block(x, (128, 128), name="block_2")
    x = conv_block(x, (256, 256), pooling=False, name="block_3")

    x = keras.layers.GlobalAveragePooling2D(name="global_average_pooling")(x)

    outputs = layers.Dense(classes, activation='softmax', name='outputs')(x)

    return Model(inputs=inputs, outputs=outputs, name=name)

Model je složen ze tří konvolučních bloků, které obsahují dvě konvoluční vrstvy následované vrstvou MaxPooling2D pro redukci prostorových dimenzí. Doposud tedy nic nového.

Ve VGG16 modelu by po konvolučních blocích obvykle následovala vrstva Flatten. V mém případě je ale nahrazena vrstvou GlobalAveragePoolong2D. Výsledkem této vrstvy je úplné potlačení prostorových dimenzí, zůstanou pouze průměrné hodnoty vlastností.

Celý model je zakončen jednou Dense vrstvou, která dělá rozlišení do jednotlivých tříd.

Pokud se podíváte do výpisu přeloženého modelu uvidíte, že jsem se postupně ze vzorků 64×64×3 konvolučními bloky dostal do vzorku 16×16×256. Odtud pak GlobalAveragePooling2D vrstva vybere průměry vlastností, tedy 256. Ty jsou pak vstupem do Dense vrstvy.

EPOCHS = 20
BATCH_SIZE = 64

model = create_model(x.shape, 2)
model.compile(optimizer="adam", loss='categorical_crossentropy', metrics=['accuracy'])
model.summary(expand_nested=True)

MODEL_CHECKPOINT = f"/kaggle/working/model/{model.name}.keras"

callbacks_list = [
    keras.callbacks.EarlyStopping(monitor='val_accuracy', patience=10),
    keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_accuracy', save_best_only=True, mode='max', verbose=1)
]

history = model.fit(x=x_train, y=y_train, epochs=EPOCHS, batch_size=BATCH_SIZE, callbacks=callbacks_list, validation_split=0.2, verbose=1)

model.load_weights(MODEL_CHECKPOINT)
Model: "Model"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ inputs (InputLayer)             │ (None, 64, 64, 3)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ data_augmentation (Sequential)  │ (None, 64, 64, 3)      │             7 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│    └ normalization              │ (None, 64, 64, 3)      │             7 │
│ (Normalization)                 │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│    └ random_flip (RandomFlip)   │ (None, 64, 64, 3)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│    └ random_rotation            │ (None, 64, 64, 3)      │             0 │
│ (RandomRotation)                │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│    └ random_zoom (RandomZoom)   │ (None, 64, 64, 3)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_conv_0 (Conv2D)         │ (None, 64, 64, 64)     │         1,792 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_norm_0                  │ (None, 64, 64, 64)     │           256 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_relu_0 (Activation)     │ (None, 64, 64, 64)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_conv_1 (Conv2D)         │ (None, 64, 64, 64)     │        36,928 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_norm_1                  │ (None, 64, 64, 64)     │           256 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_relu_1 (Activation)     │ (None, 64, 64, 64)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_1_maxpool (MaxPooling2D)  │ (None, 32, 32, 64)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_conv_0 (Conv2D)         │ (None, 32, 32, 128)    │        73,856 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_norm_0                  │ (None, 32, 32, 128)    │           512 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_relu_0 (Activation)     │ (None, 32, 32, 128)    │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_conv_1 (Conv2D)         │ (None, 32, 32, 128)    │       147,584 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_norm_1                  │ (None, 32, 32, 128)    │           512 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_relu_1 (Activation)     │ (None, 32, 32, 128)    │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_2_maxpool (MaxPooling2D)  │ (None, 16, 16, 128)    │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_3_conv_0 (Conv2D)         │ (None, 16, 16, 256)    │       295,168 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_3_norm_0                  │ (None, 16, 16, 256)    │         1,024 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_3_relu_0 (Activation)     │ (None, 16, 16, 256)    │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_3_conv_1 (Conv2D)         │ (None, 16, 16, 256)    │       590,080 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_3_norm_1                  │ (None, 16, 16, 256)    │         1,024 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ block_3_relu_1 (Activation)     │ (None, 16, 16, 256)    │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ global_average_pooling          │ (None, 256)            │             0 │
│ (GlobalAveragePooling2D)        │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ outputs (Dense)                 │ (None, 2)              │           514 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 1,149,513 (4.39 MB)
 Trainable params: 1,147,714 (4.38 MB)
 Non-trainable params: 1,799 (7.03 KB)
Epoch 1/20
276/276 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step - accuracy: 0.8318 - loss: 0.3889
Epoch 1: val_accuracy improved from -inf to 0.76825, saving model to /kaggle/working/model/Model.keras
276/276 ━━━━━━━━━━━━━━━━━━━━ 30s 70ms/step - accuracy: 0.8321 - loss: 0.3884 - val_accuracy: 0.7683 - val_loss: 0.4583
Epoch 2/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9440 - loss: 0.1675
Epoch 2: val_accuracy improved from 0.76825 to 0.93515, saving model to /kaggle/working/model/Model.keras
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 61ms/step - accuracy: 0.9440 - loss: 0.1675 - val_accuracy: 0.9351 - val_loss: 0.1696
Epoch 3/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9478 - loss: 0.1557
Epoch 3: val_accuracy did not improve from 0.93515
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9478 - loss: 0.1556 - val_accuracy: 0.7689 - val_loss: 0.6428
Epoch 4/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9488 - loss: 0.1539
Epoch 4: val_accuracy improved from 0.93515 to 0.94694, saving model to /kaggle/working/model/Model.keras
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9488 - loss: 0.1538 - val_accuracy: 0.9469 - val_loss: 0.1696
Epoch 5/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9492 - loss: 0.1503
Epoch 5: val_accuracy did not improve from 0.94694
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9492 - loss: 0.1503 - val_accuracy: 0.8807 - val_loss: 0.2883
Epoch 6/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9512 - loss: 0.1452
Epoch 6: val_accuracy improved from 0.94694 to 0.95034, saving model to /kaggle/working/model/Model.keras
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 61ms/step - accuracy: 0.9512 - loss: 0.1452 - val_accuracy: 0.9503 - val_loss: 0.1575
Epoch 7/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9517 - loss: 0.1410
Epoch 7: val_accuracy improved from 0.95034 to 0.95374, saving model to /kaggle/working/model/Model.keras
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9517 - loss: 0.1410 - val_accuracy: 0.9537 - val_loss: 0.1498
Epoch 8/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9548 - loss: 0.1345
Epoch 8: val_accuracy improved from 0.95374 to 0.95578, saving model to /kaggle/working/model/Model.keras
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9548 - loss: 0.1345 - val_accuracy: 0.9558 - val_loss: 0.1303
Epoch 9/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9552 - loss: 0.1346
Epoch 9: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9552 - loss: 0.1346 - val_accuracy: 0.9145 - val_loss: 0.2288
Epoch 10/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9564 - loss: 0.1301
Epoch 10: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9564 - loss: 0.1301 - val_accuracy: 0.9322 - val_loss: 0.1780
Epoch 11/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9549 - loss: 0.1310
Epoch 11: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9549 - loss: 0.1310 - val_accuracy: 0.9488 - val_loss: 0.1554
Epoch 12/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9561 - loss: 0.1293
Epoch 12: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9561 - loss: 0.1293 - val_accuracy: 0.9070 - val_loss: 0.2489
Epoch 13/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9583 - loss: 0.1271
Epoch 13: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9583 - loss: 0.1270 - val_accuracy: 0.9431 - val_loss: 0.1567
Epoch 14/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9585 - loss: 0.1254
Epoch 14: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9585 - loss: 0.1254 - val_accuracy: 0.8485 - val_loss: 0.3775
Epoch 15/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9570 - loss: 0.1299
Epoch 15: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9570 - loss: 0.1298 - val_accuracy: 0.9215 - val_loss: 0.2048
Epoch 16/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9624 - loss: 0.1178
Epoch 16: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9624 - loss: 0.1179 - val_accuracy: 0.9320 - val_loss: 0.1764
Epoch 17/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.9582 - loss: 0.1219
Epoch 17: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9582 - loss: 0.1218 - val_accuracy: 0.7669 - val_loss: 0.6052
Epoch 18/20
275/276 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 0.9609 - loss: 0.1200
Epoch 18: val_accuracy did not improve from 0.95578
276/276 ━━━━━━━━━━━━━━━━━━━━ 17s 60ms/step - accuracy: 0.9609 - loss: 0.1200 - val_accuracy: 0.9005 - val_loss: 0.2384

Pro trénování jsem použil celou trénovací sadu s tím, že 20% dat jsem vyčlenil pro validaci po každé dávce.

Průběh trénování je možné vidět v následujících grafech:

fig, ax = plt.subplots(1, 2, figsize=(16, 4))
sns.lineplot(data={k: history.history[k] for k in ('loss', 'val_loss')}, ax=ax[0])
sns.lineplot(data={k: history.history[k] for k in history.history.keys() if k not in ('loss', 'val_loss')}, ax=ax[1])
plt.show()

A na závěr si můžu vyzkoušet kvalitu modelu na testovací sadě dat.

Následuje tedy predikce pro testovací sadu. Výsledek je zobrazen jako „Confusion Matrix“.

y_pred = model.predict(x_test, verbose=0)

plt.figure(figsize=(6, 3))
heatmap = sns.heatmap(confusion_matrix(np.argmax(y_test, axis=-1),  np.argmax(y_pred, axis=-1)), annot=True, fmt="d", cbar=True)
heatmap.yaxis.set_ticklabels(LABELS, rotation=90, ha='right')
heatmap.xaxis.set_ticklabels(LABELS, rotation=0, ha='right')
heatmap.axes.set_ylabel('True label')
heatmap.axes.set_xlabel('Predicted label')
plt.show()

Heatmaps a lokalizace

A nyní se dostávám k podstatě tohoto článku. Pokud udělám predikci na obrázku buňky s infekcí malárie, zajímalo by mne, na základě jaké části obrázku model došel k tomuto závěru. Chtěl bych vidět, která část buňky je považována za infikovanou (jen dovětek, když se na obrázek infikované buňky podíváte, je to hned vidět).

V následujících krocích si tedy vyberu pouze ty vzorky z testovací sady, které jsou infikovány a byly správně klasifikovány (v tomto okamžiku již neřeším kvalitu modelu, pouze interpretují výsledky). Budou mne tedy zajímat pouze vzorky ve třídě 1.

Pro další vyhodnocení budu potřebovat výstup z poslední konvoluční vrstvy modelu. To se jednoduše udělá tak, že si vytvořím nový model pred_model, jehož vstupem bude vstup původního modelu. Výstupem pak bude výstup vrstvy block₃_conv₁. Tím si zajistím, že budu mít model s trénovanými vrstvami původního modelu. Výstupem jsou pak vlastnosti 16×16×256 (doporučuji podívat se do výpisu modelu výše).

Dále budu potřebovat váhy poslední klasifikační vrstvy pro třídu 1. V mém případě se váhy jmenují last_layer_weights.

PRED_CLASS = 1

pred_model = Model(model.input, model.get_layer('block_3_conv_1').output)
last_layer_weights = model.layers[-1].get_weights()[0][:, PRED_CLASS]

Vyberu si tedy náhodně několik vzorků (v tomto případě 10), které byly správně klasifikované jako infikované, a pro každý takovýto vzorek pak postupně tyto kroky:

Zobrazím si původní podobu vzorku v prvním sloupci následujícího zobrazení.
Pro tento vzorek udělám predikci pomocí modelu pred_model. Následuje dot produkt (omlouvám se, ale naznám český ekvivalent) mezi výsledkem predikce a váhami klasifikační vrstvy. Vznikne mně tak heatmap významnosti jednotlivých částí obrázku. Ještě jsem zde zařadil zvětšení obrázku na původní velikost. Výsledek je zobrazen ve druhém sloupci.
V posledním kroku jsem ještě hledal maxima ve dříve spočtené heatmap (maximálně tři na jeden obrázek). Ty mně pak poslouží k namalování čtverečku pro lepší zdůraznění místa infekce v původním obrázku.

Výsledek můžete vidět v následujícím přehledu:

samples = x_test[np.logical_and(np.argmax(y_test, axis=-1) == PRED_CLASS, np.argmax(y_pred, axis=-1) == PRED_CLASS)]

rows, cols = 10, 3
fig=plt.figure(figsize=(12, 32))
for i in range(1, rows*cols+1, 3):
    fig.add_subplot(rows, cols, i)
    image = samples[random.randrange(samples.shape[0])]

    plt.imshow(image)

    fig.add_subplot(rows, cols, i+1)

    pred_conv = pred_model.predict(np.expand_dims(image, axis=0), verbose=0)

    heat_map = np.dot(np.squeeze(pred_conv), np.expand_dims(last_layer_weights, axis=-1))
    heat_map = cv2.resize(heat_map, IMAGE_SIZE)

    plt.imshow(cv2.resize(heat_map, IMAGE_SIZE))

    fig.add_subplot(rows, cols, i+2)

    peak_coord = peak_local_max(heat_map, num_peaks=3, min_distance=5, threshold_rel=0.5)

    for h, w in peak_coord:
        plt.gca().add_patch(Rectangle((max(w-6, 0), max(h-6, 0)), 12, 12, edgecolor='r', fill=False))

    plt.imshow(image)

plt.show()

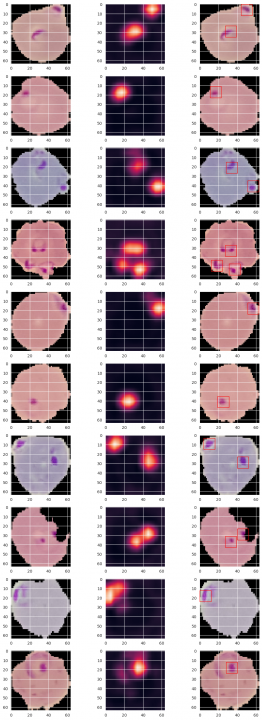
Z příkladů je vidět, že se trefuji do infikovaných míst docela dobře.

Přidejte svůj názor jako první

Datová sada

Takto vypadají neinfikované vzorky:

A takto vypadají vzorky infikované malárií:

Klasifikační model

Sdílet

Jiří Raška

Nejčtenější články autora

Poslední názory

Lokalizace infekce malárie - klasifikační model a heatmap

Datová sada

Takto vypadají neinfikované vzorky:

A takto vypadají vzorky infikované malárií:

Klasifikační model

Heatmaps a lokalizace

Sdílet

Žádné názory

Jiří Raška

Nejčtenější články autora

Poslední názory

Dále u nás najdete

Chrome OS se zřejmě promění v Android

Od pokeru do dílny: Vyrábí v ní nábytek z ohýbaného betonu

Souvisí zákaz Huawei i s nákupem stíhaček F-35?

Poznáte slavné značky a firmy jen podle loga?

Šlamastika kolem pozastavené výplaty důchodu

Edge zkouší nový trik na uživatele Chromu

Jak českým firmám pomáhá digitální transformace?

Vánoční slevy operátorů? Daleko za očekáváním

Čeští středoškoláci očekávají vypuštění své družice

První pacientka podstoupila genovou terapii bránící slepotě

Obsah vytvořený pomocí AI vidíte každý den. Jen to nevíte

Nevyžádané marketingové hovory přísnější zákon nevymýtil

Děti, které nemají praktika, mohou jít do nemocničních ordinací

Prokletí slavného spisovatele: duševní poruchy a sebevraždy

Nitroděložní tělíska jsou spolehlivá a hodí se i pro mladé ženy

Stow vytváří regálové systémy pro Alzu, Lidl i Rohlík

Novu nebude tvořit AI. A umělé moderátory v ČRo nečekejte

Lumbální punkce sice vypadá děsivě, ale nebolí

World of Warcraft slaví 20 let a stále se hraje

Řetězce falšují slevy záměrně. Měly by dostávat vyšší sankce