Lokalizace infekce malárie - AutoEncoder
V článku Lokalizace infekce malárie – klasifikační model a heatmap jsem se pokusil rozšířit výstup klasifikačního modelu o lokalizaci místa v obrázku, na základě kterého model došel ke svému závěru. Stále jsem ale vycházel z toho, že mám připravena vzorová data (obrázky) a jim odpovídající klasifikaci (metoda z kategorie Supervised learning). A v tom může být někdy zádrhel. Získání validních dat pro učení může být někdy velice pracné (obvykle jsou potřeba nějací odborníci, kteří data správně klasifikuji), a někdy získání takových dat může být úplně nereálně (z finančních nebo organizačních důvodů).
A tady by mohly pomoci metody učení z kategorie Unsupervised learning. Jednu takovou metodu si dnes vyzkouším.
Konkrétněji se jedná o metodu z oblasti Anomaly Detection, která je založena na hledání odlišností konkrétního obrázku od vzorové sady dat.
Nejdříve ale příprava prostředí:
import sys import os import shutil import warnings import glob os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' import numpy as np import matplotlib.pyplot as plt import seaborn as sns from tqdm import tqdm import tensorflow as tf import tensorflow.keras as keras from keras import Input, Model from keras import layers from sklearn.model_selection import train_test_split import cv2 sns.set_style('darkgrid') warnings.simplefilter(action='ignore', category=FutureWarning) import random def seed_all(value=42): random.seed(value) np.random.seed(value) tf.random.set_seed(value) os.environ['PYTHONHASHSEED'] = str(value) seed_all()
Datová sada
I dnes budu vycházet ze sady obrázků obsahující snímky buněk infikovaných malárií – Malaria Cell Images Dataset. Sice mám k dispozici obrázky buněk infikovaných, ale mne budou zajímat především obrázky buněk zdravých.
Snímky zdravých buněk budu používat k vytvoření referenčního modelu, se kterým pak budu porovnávat snímky buněk infikovaných. Cílem je detekovat místa, kde budou významné odlišnosti, a tedy skutečný problém.
IMAGE_ROOT = "/kaggle/input/cell-images-for-detecting-malaria/cell_images" LABELS = ['Uninfected', 'Parasitized'] IMAGE_SIZE = (128, 128)
Následuje procedura, která načítá datovou sadu do dvou samostatných numpy polí. První pole obsahuje snímky zdravých buněk, druhé pole pak snímky těch infikovaných malárií.
def get_data():
def get_subset(pathname, name=""):
images = list()
for fn in tqdm(glob.glob(pathname), desc=name):
image = cv2.imread(fn, flags=cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image = cv2.resize(image, IMAGE_SIZE).astype(np.float32) / 255.0
images.append(image)
return np.array(images)
return [get_subset(os.path.join(IMAGE_ROOT, label, '*.png'), label) for label in LABELS]
x, y = get_data()
Uninfected: 100%|██████████| 13779/13779 [02:02<00:00, 112.74it/s]
Parasitized: 100%|██████████| 13779/13779 [02:02<00:00, 112.74it/s]
Jako obvykle několik příkladů obrázků zdravých buněk:
rows, cols = 2, 5 fig=plt.figure(figsize=(14, 6)) for i in range(1, rows*cols+1): fig.add_subplot(rows, cols, i) image = x[random.randrange(x.shape[0])] plt.imshow(image) plt.show()
A nyní ještě příklady těch infikovaných:
rows, cols = 2, 5 fig=plt.figure(figsize=(14, 6)) for i in range(1, rows*cols+1): fig.add_subplot(rows, cols, i) image = y[random.randrange(y.shape[0])] plt.imshow(image) plt.show()
V posledním kroku si ještě rozdělím data na dvě sady pro trénování a testování výsledku:
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.1) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) (12401, 128, 128, 3) (12401, 128, 128, 3) (1378, 128, 128, 3) (1378, 128, 128, 3)
Model AutoEncoder
Ve svých pokusech budu dále vycházet z modelu typu AutoEncoder. Jedná se o velice často používanou metodu, kdy obrázek je několika konvolučními vrstvami zakódován do „vnitřní reprezentace“, aby byl posléze opět několika konvolučními vrstvami dekódován do původní podoby. Jádrem celého řešení je právě ta vnitřní reprezentace. Ta by měla shrnovat podstatné vlastnosti vstupních dat tak, aby jejich rekonstrukce na výstupu co nejvěrněji reprodukovala požadovaný výstup. Obvykle se model zobrazuje jako přesýpací hodiny:
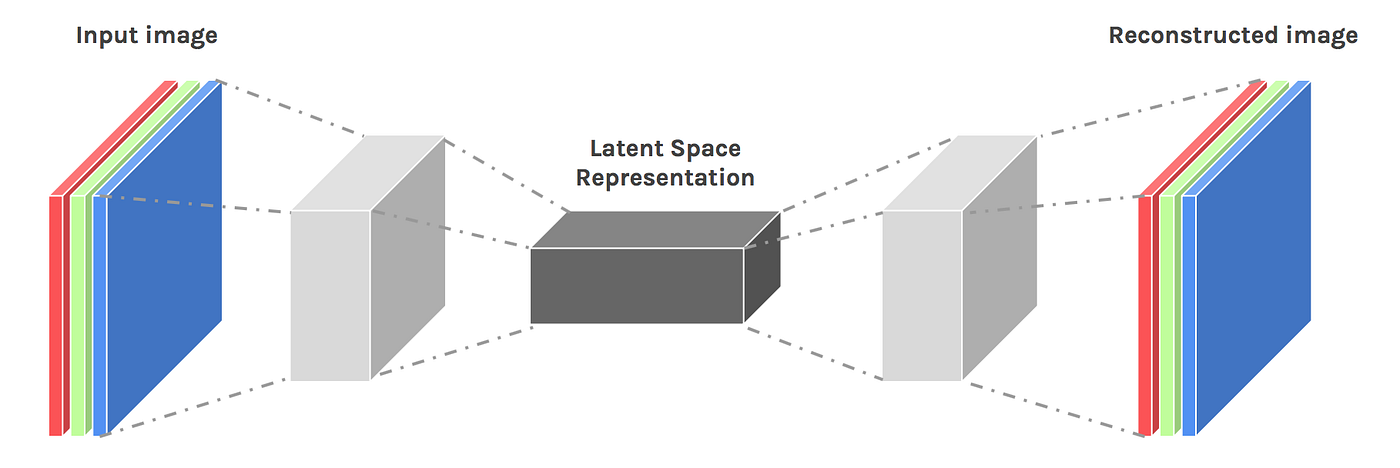
No, ale k čemu by mně tohle mohlo být dobré? Co kdybych model trénoval tak, že vstupem i výstupem bude stejný obrázek. Dostanu tak vnitřní reprezentaci, která bude shrnovat ty nejdůležitější vlastnosti vstupních dat. A co více, budu jej trénovat pouze na obrázcích buněk, které nejsou infikovány malárií.
Měl bych tak dostat model, který bude umět věrně reprodukovat obrázky zdravých buněk. No a v případě, že do něj pošlu obrázek infikované buňky, doufám, že dostanu obrázek významně odlišný od toho původního. A právě ty odlišnosti mne zajímají.
Takže nejdříve příprava modelu:
def create_model(X_shape, name="Model"):
def conv_block(x, filters, *, kernels=None, steps=None, dim_transform=None, name=""):
for i in range(len(filters)):
x = layers.Conv2D(filters[i], kernels[i] if kernels else (3, 3), strides=steps[i] if steps else (1, 1), padding='same', name=f'{name}_conv_{i}')(x)
x = layers.BatchNormalization(name=f'{name}_norm_{i}')(x)
x = layers.Activation('relu', name=f'{name}_relu_{i}')(x)
if dim_transform == 'maxpool':
x = layers.MaxPooling2D((2, 2), name=f'{name}_maxpool')(x)
elif dim_transform == "upsampl":
x = layers.UpSampling2D((2, 2), name=f'{name}_upsampl')(x)
return x
inputs = x = Input(X_shape[-3:], name='inputs')
x = conv_block(x, (64, 64), dim_transform='maxpool', name="enc_1")
x = conv_block(x, (128, 128), dim_transform='maxpool', name="enc_2")
x = conv_block(x, (256, 256), dim_transform='maxpool', name="enc_3")
x = conv_block(x, (256, 256), dim_transform='upsampl', name="dec_3")
x = conv_block(x, (128, 128), dim_transform='upsampl', name="dec_2")
x = conv_block(x, (64, 64), dim_transform='upsampl', name="dec_1")
outputs = layers.Conv2D(3, (1, 1), activation="sigmoid", padding='same', name='ouputs')(x)
return Model(inputs=inputs, outputs=outputs, name=name)
Model postavím v kontrakční i expanzní fázi na třech konvolučních blocích. Každý konvoluční blok obsahuje dvě konvoluční vrstvy následované MaxPooling2D nebo UpSampling2D vrstvou (a to podle toho, ve které jsem fázi).
Postupně tak v kontrakční fází redukuji původní dimenze obrázku 128×128×3 na vnitřní reprezentaci 16×16×256.
Následuje expanzní fáze, která mně vnitřní reprezentaci opět převádí do původní velikosti snímku.
Výstupem je konvoluční vrstva se třemi filtry pro RGB barvy, velikostí kernelu 1×1 a aktivační funkcí sigmoid.
A nyní již můžu model vytvořit, přeložit a spustit trénování:
EPOCHS = 20 BATCH_SIZE = 64 model = create_model(x.shape) model.compile(optimizer="adam", loss='mean_squared_error', metrics=['mse', 'accuracy']) model.summary(expand_nested=True) MODEL_CHECKPOINT = f"/kaggle/working/model/{model.name}.keras" callbacks_list = [ keras.callbacks.EarlyStopping(monitor='val_accuracy', patience=10), keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_mse', save_best_only=True, mode='min', verbose=1) ] history = model.fit(x=x_train, y=x_train, epochs=EPOCHS, batch_size=BATCH_SIZE, callbacks=callbacks_list, validation_split=0.2, verbose=1) fig, ax = plt.subplots(1, 2, figsize=(16, 4)) sns.lineplot(data={k: history.history[k] for k in ('loss', 'val_loss')}, ax=ax[0]) sns.lineplot(data={k: history.history[k] for k in history.history.keys() if k not in ('loss', 'val_loss')}, ax=ax[1]) plt.show() model.load_weights(MODEL_CHECKPOINT) Model: "Model" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ inputs (InputLayer) │ (None, 128, 128, 3) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_conv_0 (Conv2D) │ (None, 128, 128, 64) │ 1,792 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_norm_0 │ (None, 128, 128, 64) │ 256 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_relu_0 (Activation) │ (None, 128, 128, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_conv_1 (Conv2D) │ (None, 128, 128, 64) │ 36,928 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_norm_1 │ (None, 128, 128, 64) │ 256 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_relu_1 (Activation) │ (None, 128, 128, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_1_maxpool (MaxPooling2D) │ (None, 64, 64, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_conv_0 (Conv2D) │ (None, 64, 64, 128) │ 73,856 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_norm_0 │ (None, 64, 64, 128) │ 512 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_relu_0 (Activation) │ (None, 64, 64, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_conv_1 (Conv2D) │ (None, 64, 64, 128) │ 147,584 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_norm_1 │ (None, 64, 64, 128) │ 512 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_relu_1 (Activation) │ (None, 64, 64, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_2_maxpool (MaxPooling2D) │ (None, 32, 32, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_conv_0 (Conv2D) │ (None, 32, 32, 256) │ 295,168 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_norm_0 │ (None, 32, 32, 256) │ 1,024 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_relu_0 (Activation) │ (None, 32, 32, 256) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_conv_1 (Conv2D) │ (None, 32, 32, 256) │ 590,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_norm_1 │ (None, 32, 32, 256) │ 1,024 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_relu_1 (Activation) │ (None, 32, 32, 256) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ enc_3_maxpool (MaxPooling2D) │ (None, 16, 16, 256) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_conv_0 (Conv2D) │ (None, 16, 16, 256) │ 590,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_norm_0 │ (None, 16, 16, 256) │ 1,024 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_relu_0 (Activation) │ (None, 16, 16, 256) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_conv_1 (Conv2D) │ (None, 16, 16, 256) │ 590,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_norm_1 │ (None, 16, 16, 256) │ 1,024 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_relu_1 (Activation) │ (None, 16, 16, 256) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_3_upsampl (UpSampling2D) │ (None, 32, 32, 256) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_conv_0 (Conv2D) │ (None, 32, 32, 128) │ 295,040 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_norm_0 │ (None, 32, 32, 128) │ 512 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_relu_0 (Activation) │ (None, 32, 32, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_conv_1 (Conv2D) │ (None, 32, 32, 128) │ 147,584 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_norm_1 │ (None, 32, 32, 128) │ 512 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_relu_1 (Activation) │ (None, 32, 32, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_2_upsampl (UpSampling2D) │ (None, 64, 64, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_conv_0 (Conv2D) │ (None, 64, 64, 64) │ 73,792 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_norm_0 │ (None, 64, 64, 64) │ 256 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_relu_0 (Activation) │ (None, 64, 64, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_conv_1 (Conv2D) │ (None, 64, 64, 64) │ 36,928 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_norm_1 │ (None, 64, 64, 64) │ 256 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_relu_1 (Activation) │ (None, 64, 64, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dec_1_upsampl (UpSampling2D) │ (None, 128, 128, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ ouputs (Conv2D) │ (None, 128, 128, 3) │ 195 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 2,886,275 (11.01 MB) Trainable params: 2,882,691 (11.00 MB) Non-trainable params: 3,584 (14.00 KB) Epoch 1/20 1/155 ━━━━━━━━━━━━━━━━━━━━ 1:41:57 40s/step - accuracy: 0.4909 - loss: 0.1242 - mse: 0.1242 WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1724062437.793666 74 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process. 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.7389 - loss: 0.0145 - mse: 0.0145 Epoch 1: val_mse improved from inf to 0.03542, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 75s 229ms/step - accuracy: 0.7393 - loss: 0.0144 - mse: 0.0144 - val_accuracy: 0.6395 - val_loss: 0.0354 - val_mse: 0.0354 Epoch 2/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8412 - loss: 0.0043 - mse: 0.0043 Epoch 2: val_mse improved from 0.03542 to 0.01789, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 157ms/step - accuracy: 0.8412 - loss: 0.0043 - mse: 0.0043 - val_accuracy: 0.6122 - val_loss: 0.0179 - val_mse: 0.0179 Epoch 3/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8540 - loss: 0.0037 - mse: 0.0037 Epoch 3: val_mse improved from 0.01789 to 0.00667, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 157ms/step - accuracy: 0.8540 - loss: 0.0037 - mse: 0.0037 - val_accuracy: 0.6662 - val_loss: 0.0067 - val_mse: 0.0067 Epoch 4/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8476 - loss: 0.0033 - mse: 0.0033 Epoch 4: val_mse improved from 0.00667 to 0.00355, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 156ms/step - accuracy: 0.8476 - loss: 0.0033 - mse: 0.0033 - val_accuracy: 0.8276 - val_loss: 0.0035 - val_mse: 0.0035 Epoch 5/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8440 - loss: 0.0031 - mse: 0.0031 Epoch 5: val_mse improved from 0.00355 to 0.00306, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 157ms/step - accuracy: 0.8440 - loss: 0.0031 - mse: 0.0031 - val_accuracy: 0.8378 - val_loss: 0.0031 - val_mse: 0.0031 Epoch 6/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8403 - loss: 0.0029 - mse: 0.0029 Epoch 6: val_mse improved from 0.00306 to 0.00286, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 157ms/step - accuracy: 0.8403 - loss: 0.0029 - mse: 0.0029 - val_accuracy: 0.8261 - val_loss: 0.0029 - val_mse: 0.0029 Epoch 7/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8418 - loss: 0.0027 - mse: 0.0027 Epoch 7: val_mse improved from 0.00286 to 0.00281, saving model to /kaggle/working/model/Model.keras 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 157ms/step - accuracy: 0.8418 - loss: 0.0027 - mse: 0.0027 - val_accuracy: 0.8277 - val_loss: 0.0028 - val_mse: 0.0028 Epoch 8/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8500 - loss: 0.0027 - mse: 0.0027 Epoch 8: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 155ms/step - accuracy: 0.8500 - loss: 0.0027 - mse: 0.0027 - val_accuracy: 0.8337 - val_loss: 0.0029 - val_mse: 0.0029 Epoch 9/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 142ms/step - accuracy: 0.8603 - loss: 0.0026 - mse: 0.0026 Epoch 9: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8603 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8499 - val_loss: 0.0029 - val_mse: 0.0029 Epoch 10/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 142ms/step - accuracy: 0.8658 - loss: 0.0026 - mse: 0.0026 Epoch 10: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8658 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8487 - val_loss: 0.0030 - val_mse: 0.0030 Epoch 11/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 142ms/step - accuracy: 0.8718 - loss: 0.0026 - mse: 0.0026 Epoch 11: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8718 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8608 - val_loss: 0.0031 - val_mse: 0.0031 Epoch 12/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8791 - loss: 0.0026 - mse: 0.0026 Epoch 12: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8791 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8588 - val_loss: 0.0030 - val_mse: 0.0030 Epoch 13/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8734 - loss: 0.0026 - mse: 0.0026 Epoch 13: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8735 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8601 - val_loss: 0.0030 - val_mse: 0.0030 Epoch 14/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8780 - loss: 0.0026 - mse: 0.0026 Epoch 14: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8781 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8243 - val_loss: 0.0028 - val_mse: 0.0028 Epoch 15/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8676 - loss: 0.0026 - mse: 0.0026 Epoch 15: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8676 - loss: 0.0026 - mse: 0.0026 - val_accuracy: 0.8140 - val_loss: 0.0028 - val_mse: 0.0028 Epoch 16/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8616 - loss: 0.0025 - mse: 0.0025 Epoch 16: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8617 - loss: 0.0025 - mse: 0.0025 - val_accuracy: 0.8634 - val_loss: 0.0028 - val_mse: 0.0028 Epoch 17/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8737 - loss: 0.0025 - mse: 0.0025 Epoch 17: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 155ms/step - accuracy: 0.8738 - loss: 0.0025 - mse: 0.0025 - val_accuracy: 0.8723 - val_loss: 0.0030 - val_mse: 0.0030 Epoch 18/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8685 - loss: 0.0025 - mse: 0.0025 Epoch 18: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 155ms/step - accuracy: 0.8685 - loss: 0.0025 - mse: 0.0025 - val_accuracy: 0.8449 - val_loss: 0.0031 - val_mse: 0.0031 Epoch 19/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8751 - loss: 0.0025 - mse: 0.0025 Epoch 19: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 155ms/step - accuracy: 0.8752 - loss: 0.0025 - mse: 0.0025 - val_accuracy: 0.8539 - val_loss: 0.0029 - val_mse: 0.0029 Epoch 20/20 155/155 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.8755 - loss: 0.0025 - mse: 0.0025 Epoch 20: val_mse did not improve from 0.00281 155/155 ━━━━━━━━━━━━━━━━━━━━ 24s 154ms/step - accuracy: 0.8755 - loss: 0.0025 - mse: 0.0025 - val_accuracy: 0.8446 - val_loss: 0.0033 - val_mse: 0.0033
Jako ztrátovou funkci pro optimalizaci používám střední kvadratickou chybu (mean squared error), neboť potřebuji, aby se výstup modelu co nejméně odchyloval od vstupu.
Jen jsem vám ještě v předchozím skriptu zdůraznil dva parametry metody fit(), a sice vstupní a výstupní datová sada. Jak je vidět z výpisu, jedná se v obou případech o stejnou sadu x_train (tedy obrázky zdravých buněk).
Průběh trénování můžete vidět na následujících grafech:
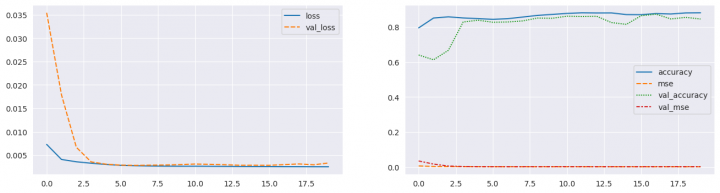
Vyhodnocení modelu
Nyní se dostávám k vyhodnocení výsledků mého modelu. Co mám tedy aktuálně k dispozici?
-
Model trénovaný na datové sadě zdravých buněk – x_train
-
Sadu snímků zdravých buněk pro ověření – x_test
-
Sadu snímků buněk infikovaných malárií pro detekci anomálií oproti těm zdravým – y_test
Pro obě testovací sady si udělám predikci:
x_pred = model.predict(x_test) y_pred = model.predict(y_test) 44/44 ━━━━━━━━━━━━━━━━━━━━ 9s 66ms/step 44/44 ━━━━━━━━━━━━━━━━━━━━ 1s 19ms/step
Nejdříve se podívám na výsledky pro testovací sadu zdravých buněk:
V prvém kroku si spočítám rozdíly mezi testovací sadou x_test a její predikcí x_pred. V tomto kroku je potřeba si uvědomit, že každý obrázek je reprezentován jako pole 128×128×3. Každý bod obrázku je vektorem o třech složkách pro základní barvy. Odečítáním tedy dostávám rozdílové vektory mezi testovací sadou a její predikcí pro každý bod. Z rozdílového vektoru mne bude ale zajímat pouze jeho velikost, a proto následuje ještě výpočet normy vektoru. V proměnné x_diff mám pro každý bode již pouze jednu hodnotu.
Vyberu si náhodně pět vzorků a výsledek si zobrazím do obrázku (komentář k jednotlivým krokům bude až pod obrázkem, aby to bylo lépe viděl):
x_diff = np.linalg.norm(x_test - x_pred, axis=-1, keepdims=True) rows, cols = 5, 4 fig=plt.figure(figsize=(16, 16)) for i in range(1, rows * cols + 1, cols): ind = random.randrange(x_test.shape[0]) # First column ... fig.add_subplot(rows, cols, i) plt.imshow(x_test[ind]) # Second column ... fig.add_subplot(rows, cols, i + 1) plt.imshow(x_pred[ind]) # Third column ... fig.add_subplot(rows, cols, i + 2) image = x_diff[ind] / x_diff[ind].max() plt.imshow(image, cmap='gray') # Fourth column ... mask = (np.linalg.norm(x_test[ind], axis=-1, keepdims=True) == 0.0).astype(np.uint16) mask = np.expand_dims(cv2.dilate(mask, np.ones((5, 5), dtype=np.uint16), iterations=1), axis=-1).astype(np.float16) mask = np.logical_not(mask).astype(np.float16) image = image * mask image = np.where(image >= 0.1, image, 0.0) image = cv2.dilate(image, np.array([[0.50, 0.75, 0.50], [0.75, 1.0, 0.75], [0.50, 0.75, 0.50]])) fig.add_subplot(rows, cols, i + 3) plt.imshow(image, cmap='gray') plt.show()
Takže co vlastně vidíte?
-
První sloupec – původní obrázek zdravé buňky z testovací sady x_test
-
Druhý sloupec – predikce zdrojového obrázku modelem
-
Třetí sloupec – normy rozdílových vektorů mezi zdrojovým obrázkem a jeho predikcí. Zde můžete vidět, že nejvýznamnější rozdíly jsou na okrajích buňky, které se nedaří rekonstruovat dokonale. Ale ony ty rozdíly jsou i v těle buňky, jen jsou špatně vidět.
-
Čtvrtý sloupec – okraje buňky mne ale moc nezajímají, proto jsem se pokusil je odstranit. Vzal jsem jako základ černé okraje snímku, které jsem ještě rozšířil o kernel 5×5 pixelů, a to celé jsem vzal jako masku pro obrázek třetího sloupce. Z výsledku jsem ještě vybral pouze ty rozdíly, které jsou větší jak 0.1 a zvýraznil je rozšířením s kernelem 3×3. Výsledek můžete vidět v tomto sloupci
Podstatný je tedy ten poslední sloupec. Pro zdravé buňky by tam nemělo být vidět nic, což se až na několik drobných odchylek skutečně ukázalo.
A nyní se stejným způsobem podívám na obrázky buněk infikovaných:
y_diff = np.linalg.norm(y_test - y_pred, axis=-1, keepdims=True) rows, cols = 10, 4 fig=plt.figure(figsize=(16, 32)) for i in range(1, rows * cols + 1, cols): ind = random.randrange(y_test.shape[0]) # First column ... fig.add_subplot(rows, cols, i) plt.imshow(y_test[ind]) # Second column ... fig.add_subplot(rows, cols, i + 1) plt.imshow(y_pred[ind]) # Third column ... image = y_diff[ind] / y_diff[ind].max() fig.add_subplot(rows, cols, i + 2) plt.imshow(image, cmap='gray') # Fourth column ... mask = (np.linalg.norm(y_test[ind], axis=-1, keepdims=True) == 0.0).astype(np.uint16) mask = np.expand_dims(cv2.dilate(mask, np.ones((5, 5), dtype=np.uint16), iterations=1), axis=-1).astype(np.float16) mask = np.logical_not(mask).astype(np.float16) image = image * mask image = np.where(image >= 0.1, image, 0.0) image = cv2.dilate(image, np.array([[0.50, 0.75, 0.50], [0.75, 1.0, 0.75], [0.50, 0.75, 0.50]])) fig.add_subplot(rows, cols, i + 3) plt.imshow(image, cmap='gray') plt.show()
Postup vyhodnocení byl stejný jako u zdravých buněk, proto jej zde nebudu detailněji popisovat.
Pohledem na poslední sloupec je zřejmé, že tady je to již daleko zajímavější. Infikovaná místa se mně daří odlišit od zbytku obrázku. Jsou zde občas zdůrazněny rozdíly v okrajích, ale to je jen u některých vzorků.
Jen bych chtěl na závěr připomenout, že model v průběhu trénování žádný obrázek s infikovanou buňkou neviděl. Takže výsledky z mého pohledu nejsou vůbec špatné.
Žádné názory
