AutoEncoder na ořechy
Ony ty AutoEncoder modely jsou na první pohled sice jednoduché, ale jejich využití je dost zajímavé. Jednou z oblastí využití je tzv. Anomaly Detection (někdy také Outlier Detection). Už jsem se této oblasti dříve dotkl, ale dnes se pokusím na ně podívat poněkud důkladněji.
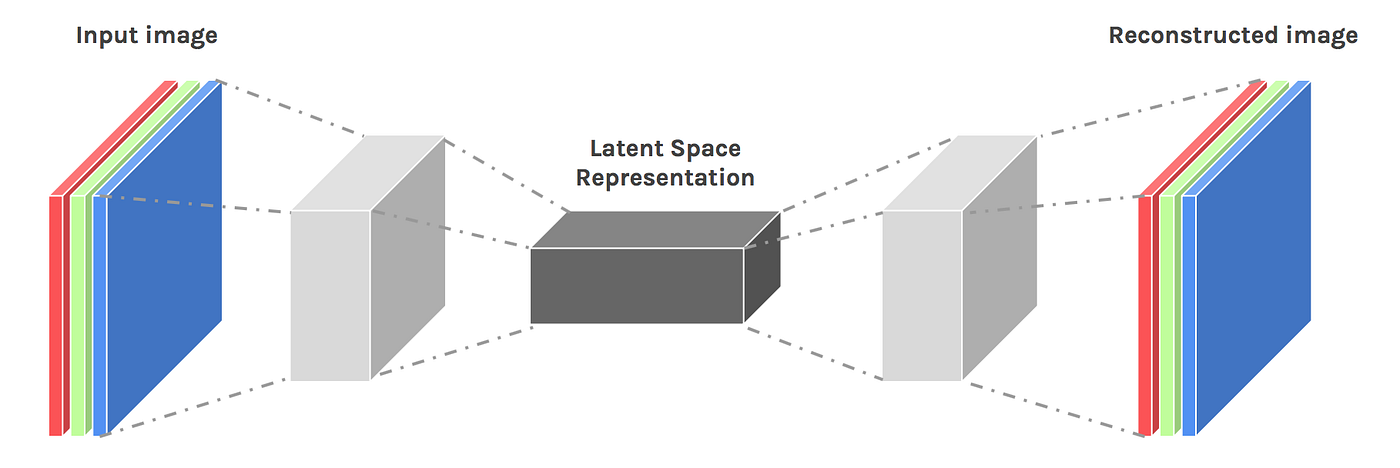
Jen pro připomenutí, každý takový AutoEncoder model má dvě části.
První je tzv. Encoder, jehož vstupem je zdrojový obrázek. Ten je postupně převáděn konvolučními vrstvami a redukcí prostorových dimenzí do vnitřní reprezentace (obvykle se označuje jako Latent Space).
Druhou částí modelu je tzv. Decoder, jehož vstupem je právě ta vnitřní reprezentace obrázku. Několika konvolučními vrstvami společně s expanzí prostorových dimenzí je postupně rekonstruována původní podoba obrázku.
Model se obvykle zobrazuje takto:
A jak mi to pomůže s detekcí anomálií?
Předpokládejme, že mám k dispozici obrázky zachycující „normální stav věci“ (pro své pokusy jsem si vybral obrázky lískových ořechů, takže mám obrázky neporušených ořechů).
Svou síť budu trénovat tak, že vstupem modelu bude obrázek „normálního stavu“ a požadovaným výstupem bude obrázek „co nejvíce podobný“ tomu vstupnímu. A co tím chci dosáhnout? Chtěl bych, aby v průběhu učení se vnitřní reprezentace naučila, jak má vypadat normální stav věci (v mém případě jak vypadá správný lískový ořech).
V případě, že do takto vytrénovaného modelu pošlu obrázek nějakým způsobem porušeného nebo deformovaného ořechu, měl bych na výstupu dostat obrázek, který se bude od toho původního významně lišit, a to především v té porušené nebo deformované části.
A o tom bude mé dnešní povídání.
Nejdříve jako obvykle příprava prostředí:
import sys, os, random, shutil, warnings, glob os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from tqdm import tqdm import tensorflow as tf import tensorflow.keras as keras from keras import layers from keras import Sequential import cv2 sns.set_style('darkgrid') warnings.simplefilter(action='ignore', category=FutureWarning) def seed_all(value=42): random.seed(value) np.random.seed(value) tf.random.set_seed(value) os.environ['PYTHONHASHSEED'] = str(value) # os.environ['TF_DETERMINISTIC_OPS'] = '1' seed_all()
Toto jsou základní parametry k datové sadě a rozlišení obrázku. V mém případě se jedná o barevné obrázky s kódování RGB, takže jejich výchozí dimenze jsou 64×64×3 hodnoty.
IMAGE_ROOT = "/kaggle/input/mvtec-ad/hazelnut"
IMAGE_SIZE = (64, 64)
Datová sada
Jak jsem již předeslal, své pokusy budu dělat na datové sadě připravené právě pro tento účel, a sice MVTec AD. Je zde k dispozici několik sad obrázků z různých oborů. Já jsem si vybral obrázky různým způsobem porušených lískových ořechů.
Mám zde již také připraveno větší množství obrázků ořechů, které jsou v pořádku. Ty jsou určeny pro trénování modelu. No a pak je tam také adresář s obrázky pro testování, zahrnující jak ořechy v pořádku, tak také ty s různými vadami.
Funkce pro načtení sady obrázků z jednoho adresáře:
def get_subset(pathname, name=""):
images = list()
for fn in tqdm(glob.glob(pathname), desc=name):
image = cv2.imread(fn, flags=cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image = cv2.resize(image, IMAGE_SIZE).astype(np.float32) / 255.0
images.append(image)
return np.array(images)
A takto si připravím data pro trénování:
x_train = get_subset(os.path.join(IMAGE_ROOT, 'train', 'good', '*.png'), 'Train images')
Train images: 100%|██████████| 391/391 [00:21<00:00, 18.25it/s]
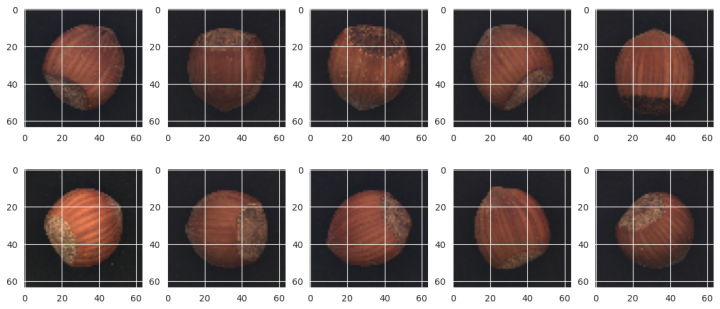
Mám k dispozici 391 obrázků lískových ořechů v obvyklém stavu. Jen pro představu několik z nich:
rows, cols = 2, 5 fig=plt.figure(figsize=(14, 6)) for i in range(1, rows*cols+1): fig.add_subplot(rows, cols, i) image = x_train[random.randrange(x_train.shape[0])] plt.imshow(image) plt.show()
AutoEncoder model
Model je postavený na konvolučních blocích jak v kontrakční, tak v expanzní fázi. Pro jednoduchost, zde je funkce pro vytvoření modelu:
def create_model(X_shape, classes=3, name="Model"):
def conv_block(x, filters, *, kernels=None, steps=None, dim_transform=None, name=""):
for i in range(len(filters)):
x = layers.Conv2D(filters[i], kernels[i] if kernels else (3, 3), strides=steps[i] if steps else (1, 1), padding='same', name=f'{name}_conv_{i}')(x)
x = layers.BatchNormalization(name=f'{name}_norm_{i}')(x)
x = layers.Activation('relu', name=f'{name}_relu_{i}')(x)
if dim_transform == 'maxpool':
x = layers.MaxPooling2D((2, 2), name=f'{name}_maxpool')(x)
elif dim_transform == "upsampl":
x = layers.UpSampling2D((2, 2), name=f'{name}_upsampl')(x)
return x
inputs = x = keras.Input(X_shape[-3:], name='inputs')
x = conv_block(x, (64, ), dim_transform='maxpool', name="enc_1")
x = conv_block(x, (128, ), dim_transform='maxpool', name="enc_2")
x = conv_block(x, (256, ), dim_transform='maxpool', name="enc_3")
x = conv_block(x, (512, ), dim_transform='maxpool', name="enc_4")
x = conv_block(x, (512, ), dim_transform='upsampl', name="dec_4")
x = conv_block(x, (256, ), dim_transform='upsampl', name="dec_3")
x = conv_block(x, (128, ), dim_transform='upsampl', name="dec_2")
x = conv_block(x, (64, ), dim_transform='upsampl', name="dec_1")
outputs = layers.Conv2D(classes, (1, 1), activation="sigmoid", padding='same', name='ouputs')(x)
return keras.Model(inputs=inputs, outputs=outputs, name=name)
model = create_model(x_train.shape, 3) model.compile(optimizer="adam", loss='mean_squared_error', metrics=['accuracy']) model.summary(line_length=110) Model: "Model" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━┩ │ inputs (InputLayer) │ (None, 64, 64, 3) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_1_conv_0 (Conv2D) │ (None, 64, 64, 64) │ 1,792 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_1_norm_0 (BatchNormalization) │ (None, 64, 64, 64) │ 256 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_1_relu_0 (Activation) │ (None, 64, 64, 64) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_1_maxpool (MaxPooling2D) │ (None, 32, 32, 64) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_2_conv_0 (Conv2D) │ (None, 32, 32, 128) │ 73,856 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_2_norm_0 (BatchNormalization) │ (None, 32, 32, 128) │ 512 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_2_relu_0 (Activation) │ (None, 32, 32, 128) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_2_maxpool (MaxPooling2D) │ (None, 16, 16, 128) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_3_conv_0 (Conv2D) │ (None, 16, 16, 256) │ 295,168 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_3_norm_0 (BatchNormalization) │ (None, 16, 16, 256) │ 1,024 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_3_relu_0 (Activation) │ (None, 16, 16, 256) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_3_maxpool (MaxPooling2D) │ (None, 8, 8, 256) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_4_conv_0 (Conv2D) │ (None, 8, 8, 512) │ 1,180,160 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_4_norm_0 (BatchNormalization) │ (None, 8, 8, 512) │ 2,048 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_4_relu_0 (Activation) │ (None, 8, 8, 512) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ enc_4_maxpool (MaxPooling2D) │ (None, 4, 4, 512) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_4_conv_0 (Conv2D) │ (None, 4, 4, 512) │ 2,359,808 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_4_norm_0 (BatchNormalization) │ (None, 4, 4, 512) │ 2,048 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_4_relu_0 (Activation) │ (None, 4, 4, 512) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_4_upsampl (UpSampling2D) │ (None, 8, 8, 512) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_3_conv_0 (Conv2D) │ (None, 8, 8, 256) │ 1,179,904 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_3_norm_0 (BatchNormalization) │ (None, 8, 8, 256) │ 1,024 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_3_relu_0 (Activation) │ (None, 8, 8, 256) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_3_upsampl (UpSampling2D) │ (None, 16, 16, 256) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_2_conv_0 (Conv2D) │ (None, 16, 16, 128) │ 295,040 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_2_norm_0 (BatchNormalization) │ (None, 16, 16, 128) │ 512 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_2_relu_0 (Activation) │ (None, 16, 16, 128) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_2_upsampl (UpSampling2D) │ (None, 32, 32, 128) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_1_conv_0 (Conv2D) │ (None, 32, 32, 64) │ 73,792 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_1_norm_0 (BatchNormalization) │ (None, 32, 32, 64) │ 256 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_1_relu_0 (Activation) │ (None, 32, 32, 64) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ dec_1_upsampl (UpSampling2D) │ (None, 64, 64, 64) │ 0 │ ├────────────────────────────────────────────────┼─────────────────────────────────────┼─────────────────────┤ │ ouputs (Conv2D) │ (None, 64, 64, 3) │ 195 │ └────────────────────────────────────────────────┴─────────────────────────────────────┴─────────────────────┘ Total params: 5,467,395(20.86 MB) Trainable params: 5,463,555(20.84 MB) Non-trainable params: 3,840(15.00 KB)
Trénování modelu
Nyní již můžu přistoupit k trénování modelu na sadě obrázků ořechů, které zachycují jejich obvyklou podobu.
Jen připomínám, všimněte si, že vstupem i výstupem je stejná datová sada.
MODEL_CHECKPOINT = f"/kaggle/working/model/{model.name}.keras"
EPOCHS = 100
callbacks_list = [
# keras.callbacks.EarlyStopping(monitor='val_accuracy', mode='max', patience=20),
keras.callbacks.ModelCheckpoint(filepath=MODEL_CHECKPOINT, monitor='val_accuracy', save_best_only=True, mode='max', verbose=1)
]
history = model.fit(
x=x_train,
y=x_train,
epochs=EPOCHS,
callbacks=callbacks_list,
validation_split=0.2,
verbose=1)
model.load_weights(MODEL_CHECKPOINT)
Epoch 1/100
7/10 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - accuracy: 0.5546 - loss: 0.0919
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1725613543.876985 73 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 754ms/step - accuracy: 0.5542 - loss: 0.0825
Epoch 1: val_accuracy improved from -inf to 0.57897, saving model to /kaggle/working/model/Model.keras
10/10 ━━━━━━━━━━━━━━━━━━━━ 24s 1s/step - accuracy: 0.5546 - loss: 0.0802 - val_accuracy: 0.5790 - val_loss: 0.1147
Epoch 2/100
8/10 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - accuracy: 0.6326 - loss: 0.0174
Epoch 2: val_accuracy improved from 0.57897 to 0.58526, saving model to /kaggle/working/model/Model.keras
10/10 ━━━━━━━━━━━━━━━━━━━━ 1s 67ms/step - accuracy: 0.6412 - loss: 0.0166 - val_accuracy: 0.5853 - val_loss: 0.1514
...
Epoch 96/100
8/10 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - accuracy: 0.9127 - loss: 7.7572e-04
Epoch 96: val_accuracy improved from 0.90850 to 0.91143, saving model to /kaggle/working/model/Model.keras
10/10 ━━━━━━━━━━━━━━━━━━━━ 1s 64ms/step - accuracy: 0.9126 - loss: 7.7291e-04 - val_accuracy: 0.9114 - val_loss: 9.6740e-04
Epoch 97/100
8/10 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - accuracy: 0.9152 - loss: 7.8558e-04
Epoch 97: val_accuracy did not improve from 0.91143
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - accuracy: 0.9128 - loss: 7.8226e-04 - val_accuracy: 0.9108 - val_loss: 9.5105e-04
Epoch 98/100
9/10 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - accuracy: 0.9172 - loss: 7.8233e-04
Epoch 98: val_accuracy did not improve from 0.91143
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - accuracy: 0.9158 - loss: 7.8089e-04 - val_accuracy: 0.9034 - val_loss: 9.6314e-04
Epoch 99/100
9/10 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - accuracy: 0.9135 - loss: 7.7903e-04
Epoch 99: val_accuracy did not improve from 0.91143
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - accuracy: 0.9132 - loss: 7.7735e-04 - val_accuracy: 0.9018 - val_loss: 9.6297e-04
Epoch 100/100
9/10 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step - accuracy: 0.9139 - loss: 7.7791e-04
Epoch 100: val_accuracy did not improve from 0.91143
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - accuracy: 0.9121 - loss: 7.7682e-04 - val_accuracy: 0.8971 - val_loss: 9.9352e-04
Výpis jsem dost zkrátil, protože vám stejně nic moc neřekne. Lepší budou grafy průběhu trénování pro ztrátovou funkci i metriku přesnosti výsledku:
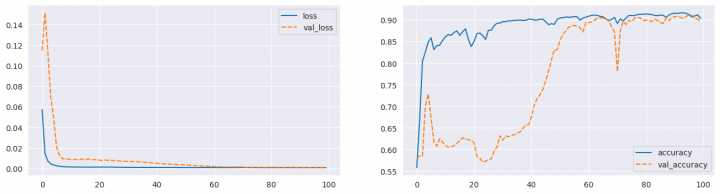
fig, ax = plt.subplots(1, 2, figsize=(16, 4)) sns.lineplot(data={k: history.history[k] for k in ('loss', 'val_loss')}, ax=ax[0]) sns.lineplot(data={k: history.history[k] for k in history.history.keys() if k not in ('loss', 'val_loss')}, ax=ax[1]) plt.show()
Vyhodnocení modelu
Když mám model vytrénovaný, mohl bych vyzkoušet, jak vypadá jeho vystup v případech, kdy mám obrázky ořechů různě deformovaných nebo porušených.
Ale v prvním kroku, jak vypadá výstup modelu v případě, že mám obrázky běžných ořechů:
LABEL = 'good' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") x_pred = model.predict(x_test) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image) plt.show() good nuts: 100%|██████████| 40/40 [00:02<00:00, 19.79it/s] 2/2 ━━━━━━━━━━━━━━━━━━━━ 3s 2s/step
Je vidět, že rekonstrukce jistě není dokonalá, ale vystihuje podstatu zdrojového obrázku.
A nyní již něco zajímavějšího, obrázky rozbitých ořechů:
LABEL = 'crack' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") x_pred = model.predict(x_test) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image) plt.show() crack nuts: 100%|██████████| 18/18 [00:00<00:00, 19.88it/s] 1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step
Z předchozího je zřejmé, že ta rekonstrukce již hodně detailů postrádá. V některých případech je ořech skutečně hodně deformovaný, jedná se tedy o velmi významné rozdíly ve velké části obrázku.
Následuje další sada testovacích obrázků, a sice ořechy s prasklinami:
LABEL = 'cut' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") x_pred = model.predict(x_test) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image) plt.show() cut nuts: 100%|██████████| 17/17 [00:00<00:00, 19.01it/s] 1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step
Zde mám tedy opačný příklad rozdílů. Praskliny jsou ve srovnání s celkovou velikostí ořechu dost malé.
A nakonec ještě jedna sada, a sice ořechy s vykousanou dírkou:
LABEL = 'hole' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") x_pred = model.predict(x_test) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image) plt.show() hole nuts: 100%|██████████| 18/18 [00:00<00:00, 20.03it/s] 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
Anomaly Detection
Takže AutoEncoder model mám připraven a vytrénován. Co tedy dále?
Zkusím vyhodnotit, zda budu schopen oddělit ty ořechy bez vad od těch, které nějakou tu vadu mají. A navíc by mne zajímalo u těch s vadou, kde ta vada dle modelu je.
Další kroky nebudu dělat na koleně, ale zkusím využít jednu z knihoven dostupných pro tento účel. Vybral jsem si knihovnu
Alibi Detect. Knihovna je obecnější, podporuje outlier, adversarial a drift detection, a to jak pro obrázky, časové řady, texty nebo tabulková data. Pokud vás tyto oblasti zajímají, součástí projektu je i dobrá dokumentace.
Knihovnu si potřebuji doinstalovat:
!pip install alibi-detect /opt/conda/lib/python3.10/pty.py:89: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock. pid, fd = os.forkpty() Collecting alibi-detect Downloading alibi_detect-0.12.0-py3-none-any.whl.metadata (28 kB) Requirement already satisfied: matplotlib<4.0.0,>=3.0.0 in /opt/conda/lib/python3.10/site-packages (from alibi-detect) (3.7.5) Requirement already satisfied: numpy<2.0.0,>=1.16.2 in /opt/conda/lib/python3.10/site-packages (from alibi-detect) (1.26.4) Requirement already satisfied: pandas<3.0.0,>=1.0.0 in /opt/conda/lib/python3.10/site-packages (from alibi-detect) (2.2.2) ... Requirement already satisfied: fsspec>=2023.5.0 in /opt/conda/lib/python3.10/site-packages (from huggingface-hub<1.0,>=0.23.2->transformers<5.0.0,>=4.0.0->alibi-detect) (2024.5.0) Requirement already satisfied: six>=1.5 in /opt/conda/lib/python3.10/site-packages (from python-dateutil>=2.7->matplotlib<4.0.0,>=3.0.0->alibi-detect) (1.16.0) Downloading alibi_detect-0.12.0-py3-none-any.whl (381 kB) ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 381.5/381.5 kB 7.8 MB/s eta 0:00:00 Installing collected packages: alibi-detect Successfully installed alibi-detect-0.12.0
Výpis je opět zkrácen, nic podstatného byste tam stejně neviděli.
from alibi_detect.od import OutlierAE THRESHOLD = 0.005 od = OutlierAE(threshold=THRESHOLD, ae=model, data_type='image')
Vytvořil jsem si OutlierAE detektor. Vstupem je v tomto případě již vytrénovaný AutoEncoder model (mohl bych jej trénovat i v rámci detektoru, ale když už jej mám, tak je to zbytečné). Jako další podstatný parametr je práh chyby THRESHOLD. Pokud výsledný obrázek překročí tento práh chyby oproti zdrojovému, je označena za outlier.
Nejdříve detektor vyzkouším na dobrých ořeších:
LABEL = 'good' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") pred = od.predict(x_test, outlier_type='instance', outlier_perc=20, return_feature_score=True, return_instance_score=True) outliers = pred['data']['is_outlier'] print(f"Correctly predicted: {(outliers == 0).sum() / len(outliers):.00%}") good nuts: 100%|██████████| 40/40 [00:01<00:00, 26.12it/s] Correctly predicted: 95%
Správně jsem označil 95% obrázků ořechů za bezproblémové.
A nyní testovací sada s rozbitými ořechy:
LABEL = 'crack' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") pred = od.predict(x_test, outlier_type='instance', outlier_perc=20, return_feature_score=True, return_instance_score=True) outliers = pred['data']['is_outlier'] print(f"Correctly predicted: {(outliers == 1).sum() / len(outliers):.00%}") x_pred = pred['data']['feature_score'] x_pred = np.linalg.norm(x_pred, axis=-1, keepdims=True) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image, cmap='gray') plt.show() crack nuts: 100%|██████████| 18/18 [00:00<00:00, 25.43it/s] Correctly predicted: 67%
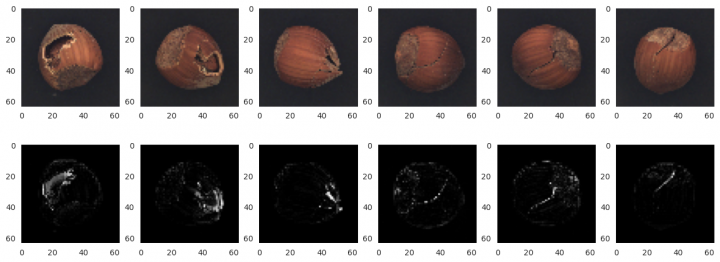
Správně jako outlier jsem označil 67% obrázků. Navíc jsem doplnil několik obrázků rozbitých ořechů s odhadem místa, kde jsou ořechy porušeny (zobrazují se tzv. feature score, tedy chyba pro konkrétní bod obrázku).
A takto to vypadá pro ořechy s prasklinami:
LABEL = 'cut' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") pred = od.predict(x_test, outlier_type='instance', outlier_perc=20, return_feature_score=True, return_instance_score=True) outliers = pred['data']['is_outlier'] print(f"Correctly predicted: {(outliers == 1).sum() / len(outliers):.00%}") x_pred = pred['data']['feature_score'] x_pred = np.linalg.norm(x_pred, axis=-1, keepdims=True) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image, cmap='gray') plt.show() cut nuts: 100%|██████████| 17/17 [00:00<00:00, 25.68it/s] Correctly predicted: 29%
V tomto případě je schopnost klasifikovat prasklé ořechy jako outlier dost slabá, konkrétně 29%. Nicméně při pohledu na feature score je vidět, že ty praskliny přece jenom nějak detekuje.
A nakonec ještě ořechy s dírkou:
LABEL = 'hole' x_test = get_subset(os.path.join(IMAGE_ROOT, 'test', LABEL, '*.png'), f"{LABEL} nuts") pred = od.predict(x_test, outlier_type='instance', outlier_perc=20, return_feature_score=True, return_instance_score=True) outliers = pred['data']['is_outlier'] print(f"Correctly predicted: {(outliers == 1).sum() / len(outliers):.00%}") x_pred = pred['data']['feature_score'] x_pred = np.linalg.norm(x_pred, axis=-1, keepdims=True) rows, cols = 3, 6 fig=plt.figure(figsize=(16, 9)) for i, ind in enumerate(random.sample(range(x_pred.shape[0]), cols)): fig.add_subplot(rows, cols, i + 1) image = x_test[ind] plt.grid(False) plt.imshow(image) fig.add_subplot(rows, cols, i + cols + 1) image = x_pred[ind] plt.grid(False) plt.imshow(image, cmap='gray') plt.show() hole nuts: 100%|██████████| 18/18 [00:00<00:00, 25.59it/s] Correctly predicted: 72%
Úspěšnost klasifikace je v tomto případě docela dobrá. Je to těch 72%. Navíc lokalizace těch dírek je překvapivě přesná. Ono to bude souviset s tím, že ty dírky jsou dost vizuálně významné.
-
Super článek. Ještě by to chtělo vysvětlení ke kódu , co to vlastně za knihovny a moduly v pythonu, k čemu daný modul slouží, protože se to tam importy hemží jen.
Pro úplné analfebetyJo, a na čem probíhá výpočet(jednodtlivé fáze)? Cpu, gpu, tpu? Trvá nějaký krok déle než sekundu výpočetního Času?
Pokud ne na cpu, nikde tam nevidím výběr(zvolení) a inicializaci daného device.
ČLÁNKY DO MAILU