Jak spočítat přeponu trojúhelníka
Jak spočítat přeponu trojúhelníka? Zdánlivě banální otázka. Od Pythagorových dob je na ni poměrně jednoduchá odpověď. c2=a2+b2. Ovšem Pythagoras netušil, že odmocnina je pro malé procesory velký problém.
Při hraní si s firmwarem k reprapu jsem se dostal k zajímavému zjednodušení tohoto problému. Firmware totiž musí spočítat, jaká je vzdálenost, kterou musí ujet hlavička mezi body (x1,y1) a (x2,y2). Ve zdrojových kódech jsem našel tento zajímavý link:
http://www.flipcode.com/archives/Fast_Approximate_Distance_Functions.shtml
V zásadě jde o náhradu Pythagorovského výpočtu přepony pouze sčítáním a násobením.
Trochu jsem tento výpočet upravil, abych dosáhl vyšší přesnosti při zachování jednoduchosti algoritmu.
Jako první operace se udělá absolutní hodnota souřadnic X a Y a porovná se, která souřadnice (t.j. strana trojúhelníka) je větší. Pokud je Y vetší než X, souřadnice se navzájem přehodí. Na délku přepony to samozřejmě nemá vliv, ovšem zaručili jsme, že jakákoliv kombinace souřadnic se transformuje na trojúhelník se úhlem menším nebo rovném 45 stupňům.
Pokud si zvolíme stranu X například 100 a stranu Y od 0 do 100, délka přepony jako funkce délky strany Y je křivka, která se dá poměrně úspěšně proložit dvěma přímkami se zlomem v polovině.
V následujícím kroku se tedy zjistí, jestli je strana Y menší než polovina strany X, to znamená, jestli je úhel menší než přibližně 27 stupňů a podle výsledku testu se použije jedna nebo druhá kombinace konstant pro výpočet délky přepony. Nakonec se připočítá 128 kvůli zaokrouhlování a zrotujeme 8 krát doprava, protože konstanty pro násobení jsou násobeny právě 256ti (reálně jsou všechny menší než 1).
Trochu jsem si pohrál s těmito konstantami a našel jsem hodnoty o které se s vámi chci podělit.
Celá funkce se dá napsat takto:
int32_t prepona(int32_t a, int32_t b)
{
if (a<0) a=-a;
if (b<0) b=-b;
if (a<b) { int32_t x=a; a=b; b=x; } // make A greater than B
if (a>(b<<1)) return (253*a+ 58*b+128)>>8;
else return (208*a+152*b+128)>>8;
}
Algoritmus používá pouze rotace, násobení a sčítání. Žádné dělení ani odmocňování není zapotřebí, takže je ideální pro mikrocontrollery. Přesnost algoritmu samozřejmě není závratná, ale pro žádný trojúhelník, který je dostatečně velký, aby se neprojevila chyba quantizace integeru, není chyba výpočtu větší než 1.5%, směrodatná odchylka je 0.66%.
Samozřejmě, že pokud bych počítal přeponu příliš malého trojúhelníka, například a=1, b=1, výsledek bude úplně mimo – bude 1 nebo 2, protože pracujeme s integery. V takovém případě ovšem stačí vynásobit obě souřadnice stejnou hodnotou, například 256 a dostaneme výsledek s maximální přesností algoritmu, samozřejmě zase vynásobený stejnou hodnotou, v tomto případě 256.
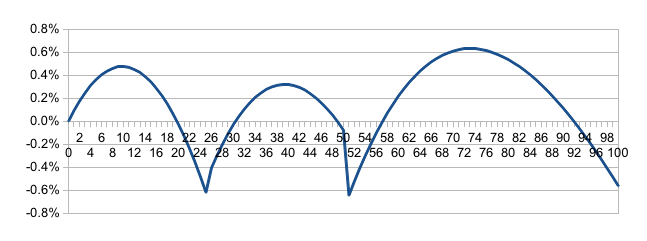
Toto je graf chyby výpočtu v závislosti na poměru stran a,b.
Na základě komentářů a taky díky tomu, že jsem o problematice dále přemýšlel, ještě jsem algoritmus dále vylepšil.
Rozdělil jsem první polovinu na další 2 části. Výsledek má několik zajímavých vlastností.
- největší chyba se snížila na přibližně 0.6%, směrodatná odchylka je nyní 0.33%
- trojúhelník s nulovým úhlem = stav kdy hlavička jede horizontálně nebo vertikálně se vypočítává s absolutní přesností
- v případě, že má trojúhelník větší poměr stran než 1:4 se dokonce ušetří jedno násobení, protože konstanta pro stranu A je 256 (reálně 1.000000)
graf relativní chyby výpočtu přepony s upraveným algoritmem
A teď už konečně ten upravený program:
int prepona(int a, int b)
{
if (a<0) a=-a;
if (b<0) b=-b;
if (a<b) { int x=a; a=b; b=x; }
if (a>=(b<<2)) return a+((25*b+128)>>8);
if (a>=(b<<1)) return (240*a+ 92*b+128)>>8;
else return (208*a+152*b+128)>>8;
}
Kdo si chce hrát, tady si může stáhnout tabulku kterou jsem používal na hledání koeficientů.
prepona-3parts.ods Musíš jenom přejmenovat file na cokoliv.ods. Musel jsem to nahrát jako obrázek png, protože tenhle blogovací site neumožňuje nahrát cokoliv jiného než obrázky. Na cokoliv jiného to vyhlásí, že je ten file nebezpečný. :-(
-
Související články na blogu Jet
-
Počítání s přetečením v C 1. 10. 2014 23:30
-
-
Související články na ostatních blozích
-
Vzdálený ROOT v Cisco routrech 16. 6. 2016 12:47
-
-
trsek (neregistrovaný)
Sqrt je mozne pekne riesit aj pomocou Newtonovho algoritmu.
Riesil som to v pascale na tzv. BigNumbers.
Pochvalim sa:
http://www.trsek.com/pas/math.pas&inf=pas.inf/1inca.inf -
Ondrej Certik (neregistrovaný)
V Pythonu jsem taky jednou napsal sqrt() pomoci Newtonovy metody:
def sqrt(x):
eps = 1e-10
x = float(x)
r = x/2
residual = r**2 - x
while abs(residual) > eps:
r -= residual/(2*r)
residual = r**2 - x
return rPro predstavu, je potreba radove 5 iteraci pro presnost 1e-10 pro cisla kolem 10.
Pro integery jsem udelal tuto verzi pomoci Newtonovy metody:
def prep2(a, b):
x = a**2 + b**2
r = x/2
residual = r**2 - x
r_old = r+1
while 1:
r -= residual/(2*r)
residual = r**2 - x
if r == r_old:
break
r_old = r
return rPouziva se jen integer division. Melo by to byt presny +-1 (integer). Porad to ale vypada pomalejsi nez ten trik v blogu.
-
Ondrej Certik (neregistrovaný)
Root zkazil formatovani, takze predchozi prispevek jeste jednou. V Pythonu jsem taky jednou napsal sqrt() pomoci Newtonovy metody:
https://gist.github.com/996210
Pro predstavu, je potreba radove 5 iteraci pro presnost 1e-10 pro cisla kolem 10.
Pro integery jsem udelal tuto verzi pomoci Newtonovy metody:
https://gist.github.com/996213
Pouziva se jen integer division. Melo by to byt presny +-1 (integer). Porad to ale vypada pomalejsi nez ten trik v blogu.
-
Jet (neregistrovaný)
[4] - dobrá myšlenka, ale problém je v tom, že výsledek už bude záležet i na absolutní velikosti trojúhelníka. S původním algoritmem na tom nezáleží, protože je lineární. Trojúhelník 3x4 má přeponu 5, trojúhelník 2 krát vetší - 6x8 má 2 krát větší přeponu - 10. Pokud bych do toho zatáhl parabolu, přepona druhého trojúhelníka nebude 2 krát větší, ale o něco víc. Takže tahle idea bohužel není použitelná.
-
dolik.rce (neregistrovaný)
[5] - Pravda, zapomel jsem ze by bylo potreba jedno deleni kvuli skalovani, ale pokud prejdeme tento drobny nedostatek, tak to samozrejme realizovat lze. Jako dukaz viz funkci prepona2 na http://pastebin.com/DsJzw2tG (sorry, ale jsem liny zjistovat jak v komentari formatovat kod ;-) ). Presnost je vyssi, ale deleni s sebou ovsem prinasi drobnou penalizaci vykonu, nameril jsem zhruba o 25% delsi cas vypoctu. I to lze ovsem spravit, pokud se zbavíme pomerne náročného if, a pouzijeme aproximaci parabolou na celem oboru, viz predchozi link, funkce prepona3. Tato funkce je dokonce o neco rychlejsi nez puvodni original a ma i vyssi presnost. Abych sva slova podlozil, prikladam i grafy presnosti: http://i54.tinypic.com/2ezqwow.png
Tak uz mi verite ze to je pouzitelne? :-)
-
dolik.rce (neregistrovaný)
PS: Omlouvam se za omyl, co se te rychlosti tyce jsem kecal... Az po odeslani jsem si uvedomil, ze jsem pouzil spatnou metodiku mereni a dostal jsem naprosto nereevantni casy. Po oprave mi vychazi zhruba nasledujici:
prepona3: 69.80 ns
prepona2: 47.80 ns
prepona: 25.80 ns
Tedy puvodni funkce je nejrychlejsi a deleni si tvrde vybira svou dan... Narust presnosti je zaplacen rychlosti, ale to uz tak bohuzel v zivote byva :) -
Jet (neregistrovaný)
[dolik.rce] vypada to zajimave, ale prece jenom, je to uz slozite. Mrkni jeste jednou na clanek, mezitim jsem ho updatnul. Na zaklade tveho komentare cislo 4 jsem s tim jeste trochu laboroval a dostal jsem se na priblizne pul procenta (coz je mimo jine srovnatelne s tvoji funkci prenona3.
Tento algoritmus je urcen predevsim pro male processory (treba PIC), ja ho pouzivam na ARMu. Na techto processorech je uz jenom jednoduche deleni pomerne velky problem. Takze algoritmus, ve kterem jsou 3 porovnavani, 3 rotace, 2 nasobeni a zbytek jenom scitani a hlavne zadna smycka, muze byt radove 100 krat rychlejsi nez klasicky vypocet pres mocniny a odmocniny. Nehlede samozrejme na delku kodu. -
dolik.rce (neregistrovaný)
Jasny, chapu. Vzdycky je to o tom najit ten spravny pomer 'cena/vykon' pro danou aplikaci...
Mimochodem, ciste ze zedavosti, jak urcujes optimalni koeficienty? Ja jsem si napocital par bodu pro tu aproximovanou funkci a pak vzal koeficienty spocitany linearni regresi, ale vzhledem k tomu ze tady jde o celociselne operace, tak mi to neprijde uplne bezpecne. Mohly by existovat i lepsi...
-
Jet (neregistrovaný)
Šel jsem na to "vědecky" :-). Udělal jsem si tabulku ve spreadsheetu a koeficienty jsem našel ručně. Vypadá to sice jako zdlouhavé řešení, ale jde to celkem rychle. Každý z nich má určitý konkrétní vliv na výslednou křivku, takže to jde poměrně rychle. Dalo by se to samozřejmě řešit lineární regresí jak jsi už zmiňoval, ale než bych napsal funkci, která by to rozdělila na 3 čáasti a počítala regrese, měl jsem koeficienty nalezeny ručně. Je to i zábavnější :-)
Tabulku jsem přidal do článku, můžes si taky pohrát. -
Karel (neregistrovaný)
Někdy se o přeponě a odvěsnách mluví i u nepravoúhlých trojúhelníků (ve smyslu přepona = nejdelší hrana), ale zaprvé to není odborný termín a zadruhé tam neplatí Pythagorova věta. Zahradník se holt bez goniometrických funkcí neobejde i kdyby té cestičce kolem růží stokrát říkal přepona :-)
-
St (neregistrovaný)
Chlapci, běžte na http://www.tichanek.cz/g1v/Iv.html
Tam jsou na přepony a na Pythagora názory... -
Jet (neregistrovaný)
Spravna pripominka. Schizu uz mam davno. Ja mluvim cesky, manzelka slovensky, deti italsky a komentare pisu anglicky, aby to po me jeste nekdo mohl cist :-)Spis je nahoda, ze jsem tu funkci pojmenoval cesky :-)
Jeste se omlouvam, ze pisu bez hacku a carek, protoze psat s hackama a carkama je pro me opravdu utrpeni. Ten clanek jsem psal priblizne 3 krat dele nez kdybych to psal bez hacku a carek.
-
logik (neregistrovaný)
A co todle?
http://www.dspcsp.com/progs/pythsum.c.txt
konverguje to kvadraticky. Akorát to je pro floaty, nechce se mi teď přemejšlet,
jakej problém je to upravit pro integery. Používá se to ve výpočtech, kdy by
prostý počítání pomocí mocnin mohlo výst k přetečení.
